Pestalozzi Gymnasium Biberach EduRandomtasks

orthogonale Vektoren

Beispiel:

Für welches a sind die beiden Vektoren $\vec{a}$ = $(\begin{matrix} 3 \\ -3 \\ 0 \end{matrix})$ und $\vec{b}$ = $(\begin{matrix} -9 \\ a \\ -3 \end{matrix})$ orthogonal ?

Lösung einblenden

Damit die beiden Vektoren orthogonal sind, muss ihr Skalarprodukt =0 sein

Also: $\vec{a}$ ⋅ $\vec{b}$ = $(\begin{matrix} 3 \\ -3 \\ 0 \end{matrix})$ ⋅ $(\begin{matrix} -9 \\ a \\ -3 \end{matrix})$ = $3 \cdot (-9) + (-3) \cdot a + 0 \cdot (-3)$ = -27 + -3a =0

-3a = 27 |:-3

a = -9

gemeinsame Ebene einer Geradenschar1

Beispiel:

Gegeben ist eine Geradenschar g_a durch $\vec{x} =$ $(\begin{matrix} 3 \\ -5 \\ 1 \end{matrix}) + t \cdot (\begin{matrix} 6 \\ a \\ -4 \end{matrix})$ .

Bestimme eine Ebene, in der alle Geraden der Geradenschar g_a liegen.

Lösung einblenden

Alle Geraden der Schar haben den selben Aufpunkt, haben aber verschiedene Richtungsvektoren.

Wenn es einen Ebene gibt, in der alle Geraden liegen, so muss diese einen Normalenvektor besitzen, der orthogonal zu all diesen verschiedenen Richtungsvektoren ist.

Es muss also gelten: $(\begin{matrix} 6 \\ a \\ -4 \end{matrix})$ ⋅ $(\begin{matrix} n_{1} \\ n_{2} \\ n_{3} \end{matrix})$ =0

Da in der x₂-Koordinate des Richtungsvektors der Parameter jeden beliebigen Wert annehmen kann, muss der n₂-Wert des Normalenvektor =0 sein, so hat das Skalarprodukt für jedes verschiedene a den selben Wert. Um diesen Wert jetzt auch noch auf 0 zu bekommen, müssen wir einfach die anderen beiden Koordinaten vertauschen und bei einem noch das Vorzeichen wechseln.

Also $\vec{n}$ = $(\begin{matrix} -4 \\ 0 \\ -6 \end{matrix})$ oder $\vec{n}$ = $(\begin{matrix} 2 \\ 0 \\ 3 \end{matrix})$ = $- \frac{1}{2}$ $(\begin{matrix} -4 \\ 0 \\ -6 \end{matrix})$ , denn $(\begin{matrix} 6 \\ a \\ -4 \end{matrix})$ ⋅ $(\begin{matrix} 2 \\ 0 \\ 3 \end{matrix})$ =0, für jedes beliebige a.

Die gesuchte gemeinsame Ebene hat also die Form: $2 x_{1} + 3 x_{3} = d$ .

Jetzt brauchen wir nur noch einen Punkt dieser Ebene, um das Absolutglied d noch zu bestimmen. Dafür können wir ja den Aufpunkt von g_a $(3 | -5 | 1)$ nehmen. Denn dieser ist ja für jedes a gleich, also auf jeder Geraden g_a und somit auch auf der gesuchten gemeinsamen Ebene E.

Eingesetzt in die bisherige Ebenengleichung erhalten wir $2 \cdot 3 + 0 \cdot (-5) + 3 \cdot 1$ =9=d

Die gesuchte gemeinsame Ebenen hat also die Gleichung: $2 x_{1} + 3 x_{3} = 9$

gemeinsame Gerade einer Ebenenschar

Beispiel:

Gegeben ist eine Ebenenschar E_a durch E_a: $-5 x_{1} + x_{2} + a x_{3} = 5a$ .

Zeige, dass sich alle Ebenen in einer Geraden schneiden. Bestimme diese Schnittgerade.

Lösung einblenden

Wenn es eine Geraden gibt, die in allen Ebenen der Schar liegt, so muss deren Richtungsvektor $(\begin{matrix} r_{1} \\ r_{2} \\ r_{3} \end{matrix})$ orthogonal zu allen Normalenvektoren der verschiedenen Ebenen der Schar sein, weil eben alle Vektoren einer Ebene immer orthogonal zum Normalenvektor der Ebene sind.

Es muss also gelten: $(\begin{matrix} r_{1} \\ r_{2} \\ r_{3} \end{matrix})$ ⋅ $(\begin{matrix} -5 \\ 1 \\ a \end{matrix})$ =0

Um das Ergebnis des Skalarprodukts unabhängig von a zu bekommen, setzen wir r₃ einfach mal =0. Für die anderen beiden Werte r₁ und r₂ nehmen wir einfach die jeweils andere Koordinate des Normalenvektors und drehen bei einem noch das Vorzeichen, so dass das Skalarprodukt auf jeden Fall Null ergibt.

Also : $(\begin{matrix} 1 \\ 5 \\ 0 \end{matrix})$ ⋅ $(\begin{matrix} -5 \\ 1 \\ a \end{matrix})$ =0. Der Richtungsvektor $\vec{r}$ = $(\begin{matrix} 1 \\ 5 \\ 0 \end{matrix})$ steht also senkrecht auf allen Normalenvektoren und ist damit in allen Ebenen E_a enthalten.

Jetzt brauchen wir noch einen Stützvektor der gemeinsamen Geraden, also den Ortsvektor zu einem Punkt, der in allen Ebenen E_a liegt, also einen Punkt, der die Ebenengleichung E_a: $-5 x_{1} + x_{2} + a x_{3} = 5a$ für jedes a erfüllt.

Da auf der rechten Seite der Ebenegleichung 5a steht, müssen wir einfach x₃=5 und die anderen beiden Koordianten auf 0 setzen.

So erhalten wir also den Punkt $(0 | 0 | 5)$ , der auf jeder Ebene E_a liegt, denn eingesetzt in E_a erhalten wir: 5a = 5a.

$(\begin{matrix} 0 \\ 0 \\ 5 \end{matrix})$ ist also unser gesuchter Stützvektor.

Die gesuchte Gerade ist also g: $\vec{x} =$ $(\begin{matrix} 0 \\ 0 \\ 5 \end{matrix}) + t \cdot (\begin{matrix} 1 \\ 5 \\ 0 \end{matrix})$

(Zur Kontrolle kann man übrigends den allgemeinen Geradenpunkt der Lösungsgeraden wieder in die Ebenegleichung E_a einsetzen und es muss 0=0 herauskommen)

gegebener Abstand zu Punkt

Beispiel:

Gegeben ist eine Ebenenschar E_a durch E_a: $-6 x_{1} + 2 x_{2} + a x_{3} = 18$ .

Für welche(s) a hat der Punkt $(21 | -10 | 49)$ den Abstand 55 von der Ebene E_a?

Lösung einblenden

Nach der Hesse'schen Normalenform muss gelten:

$\frac{| -6 \cdot 21 +2 \cdot (-10) +a \cdot 49 - 18 |}{\sqrt{{(-6)}^{2} + 2^{2} + a^{2}}}$ = 55

Wir multiplizieren mit der Wurzel im Nenner durch:

$| 49 a - 164 |$ = 55⋅ $\sqrt{{(-6)}^{2} + 2^{2} + a^{2}}$

vereinfacht:

$| 49 a - 164 |$ = $55 \sqrt{a^{2} + 40}$

Jetzt wird auf beiden Seiten quadriert:

(Vorsicht: Hier wird zwar auf beiden Seiten quadriert. Da aber auch links Beträge stehen, ist sowohl die negative als auch die postive Wurzel bereits vorher in der Lösungsmenge. Sie wird also nicht vergrößert. Eine Probe ist also ausnahmsweise nicht erforderlich)

${(49 a - 164)}^{2}$ = $3 025 (a^{2} + 40)$

$2 401 a^{2} - 16 072 a + 26 896$ = $3 025 a^{2} + 121 000$

2 401 a^{2} - 16 072 a + 26 896

=

3 025 a^{2} + 121 000

|

- 3 025 a^{2}

- 121 000

- 624 a^{2} - 16 072 a - 94 104

= 0 |:8

$- 78 a^{2} - 2 009 a - 11 763$ = 0

eingesetzt in die Mitternachtsformel (a-b-c-Formel):

a_1,2 = $\frac{+ 2 009 \pm \sqrt{{(- 2 009)}^{2} - 4 \cdot (- 78) \cdot (- 11 763)}}{2 \cdot (- 78)}$

a_1,2 = $\frac{+ 2 009 \pm \sqrt{4 036 081 - 3 670 056}}{- 156}$

a_1,2 = $\frac{+ 2 009 \pm \sqrt{366 025}}{- 156}$

a₁ = $\frac{2 009 + \sqrt{366 025}}{- 156}$ = $\frac{2 009+605}{- 156}$ = $\frac{2 614}{- 156}$ = $- \frac{1307}{78}$ ≈ -16.76

a₂ = $\frac{2 009 - \sqrt{366 025}}{- 156}$ = $\frac{2 009-605}{- 156}$ = $\frac{1 404}{- 156}$ = $- 9$

Gerade schneidet x-Achse

Beispiel:

Gegeben ist eine Geradenschar g_a durch $\vec{x} =$ $(\begin{matrix} -13 \\ -10 \\ 20 \end{matrix}) + t \cdot (\begin{matrix} -3 \\ -2 \\ a \end{matrix})$ .

Für welches a schneidet g_a die x₁-Achse?

Lösung einblenden

Die x₁-Achse hat die Geradengleichung $\vec{x} =$ $(\begin{matrix} 0 \\ 0 \\ 0 \end{matrix}) + t \cdot (\begin{matrix} 1 \\ 0 \\ 0 \end{matrix})$ . Um einen Schnittpunkt der beiden Geraden zu finden, setzen wir sie gleich

;

$(\begin{matrix} -13 \\ -10 \\ 20 \end{matrix}) + s \cdot (\begin{matrix} -3 \\ -2 \\ a \end{matrix})$ = $(\begin{matrix} 0 \\ 0 \\ 0 \end{matrix}) + t \cdot (\begin{matrix} 1 \\ 0 \\ 0 \end{matrix})$

Als Gleichungssystem geschrieben:

$\begin{matrix} -13 & -3 s & = & 0 & +1 t \\ -10 & -2 s & = & 0 & +0 t \\ 20 & +a s & = & 0 & +0 t \end{matrix}$

Wir betrachten erstmal die beiden Gleichungen ohne Parameter und formen diese so um, dass man das LGS gut lösen kann.

\begin{matrix} - 3 s & - 1 t & = & 13 & (I) \\ - 2 s & = & 10 & (II) \end{matrix}

\begin{matrix} - 3 s & - 1 t & = & 13 & (I) \\ - 2 s & = & 10 & (II) \end{matrix}

langsame Rechnung einblenden $2$ ·(I) $- 3$ ·(II)

\begin{matrix} - 3 s & - 1 t & = & 13 & (I) \\ (- 6 + 6) s & + (- 2 + 0) t & = & (26 - 30) & (II) \end{matrix}

\begin{matrix} - 3 s & - 1 t & = & 13 & (I) \\ - 2 t & = & - 4 & (II) \end{matrix}

Zeile (II):

\begin{matrix} - 2 t & = & - 4 \end{matrix}

t = $2$

eingesetzt in Zeile (I):

\begin{matrix} - 3 s & - 1 (2) & = & 13 \end{matrix}

| +

2

- 3

s =

15

| :

(-3)

s = $- 5$

$L = {(- 5 | 2)}$

Jetzt setzen wir die Lösung s= $- 5$ in die 3-te Gleichung des ursprünglichen Gleichungssystems ganz oben ein:

20 + a⋅(-5) = 0 |-20

-5a = -20 | :(-5)

a = 4

der Schnittpunkt wäre dann $\vec{OS}$ = $(\begin{matrix} -13 \\ -10 \\ 20 \end{matrix})$ -5⋅ $(\begin{matrix} -3 \\ -2 \\ 4 \end{matrix})$ = $(\begin{matrix} 2 \\ 0 \\ 0 \end{matrix})$

gegebener Steigungswinkel

Beispiel:

Gegeben ist die Geradenschar g_a durch g_a: $\vec{x} =$ $(\begin{matrix} -1 \\ -5 \\ 5 \end{matrix}) + t \cdot (\begin{matrix} -3 \\ 4 \\ a \end{matrix})$ .

Für welches a>0 hat die Gerade g_a den Steigungswinkel α=21.8°?

Lösung einblenden

Als Steigungswinkel wird der Winkel zwischen der Geraden und der horizontalen Grundebene, also der x₁x₂-Ebene bezeichnet. Der Normalenvektor, x₁x₂-Ebene steht natürlich senkrecht nach oben, hat also die Koordinaten $\vec{n}$ = $(\begin{matrix} 0 \\ 0 \\ 1 \end{matrix})$

Nach der Formel für den Winkel zwischen einer Geraden mit dem Richtungsvektor $(\begin{matrix} -3 \\ 4 \\ a \end{matrix})$ und einer Ebene mit dem Normalenvektor $(\begin{matrix} 0 \\ 0 \\ 1 \end{matrix})$ muss also gelten:

sin(21.8°)= $\frac{| (-3) \cdot 0 + 4 \cdot 0 + a \cdot 1 |}{\sqrt{{(-3)}^{2} + 4^{2} + a^{2}} \cdot \sqrt{0^{2} + 0^{2} + 1^{2}}}$

sinus ausgerechnet (Vorsicht: Gradmaß, nicht Bogenmaß) und rechts vereinfacht:

0.3714 = $\frac{|a|}{\sqrt{a^{2} + 25}⋅ 1}$

Wir multiplizieren mit der Wurzel im Nenner durch:

$0,3714 \sqrt{a^{2} + 25}$ = |a|

Jetzt wird auf beiden Seiten quadriert:

(Vorsicht: Hier wird zwar auf beiden Seiten quadriert. Es könnte also eine Scheinlösung der Gleichung $0,3714 \sqrt{a^{2} + 25}$ = -|a| hinzukommen. Diese kann aber keine Lösung haben, da die linke Seite immer positiv und die rechte immer negativ ist. Es kann also keine falsche Lösung hinzukommen, somit ist eine Probe nicht erforderlich)

$0,1379 (a^{2} + 25)$ = $a^{2}$

$0,1379 a^{2} + 3,4475$ = $a^{2}$

$0,1379 a^{2} + 3,4475$	=	$a^{2}$	\| $- 3,4475$ $- a^{2}$
$- 0,8621 a^{2}$	=	$- 3,4475$	\|: $(- 0,8621)$
$a^{2}$	=	$3,99896$	\| $\sqrt[2]{\cdot}$
a₁	=	$- \sqrt{3,99896}$	≈ $- 2$
a₂	=	$\sqrt{3,99896}$	≈ $2$

Für a= $2$ ≈ 2 ist der Steigungswinkel also 21.8°.

Parameter für Schnittpunkt wählen

Beispiel:

Gegeben ist eine Geradenschar g_a durch $\vec{x} =$ $(\begin{matrix} a \\ -21 \\ 5 \end{matrix}) + t \cdot (\begin{matrix} 5 \\ 5 \\ -2 \end{matrix})$ und eine Gerade h mit h: $\vec{x} =$ $(\begin{matrix} 22 \\ 29 \\ 10 \end{matrix}) + t \cdot (\begin{matrix} 4 \\ 5 \\ 3 \end{matrix})$ .

Für welchen Wert von a sind g_a und h nicht windschief?

Lösung einblenden

Man erkennt sofort an den Richtungsvektoren, dass die beiden Geraden nicht parallel oder gar identisch sein können.

Sie können also nur windschief sein oder sich in einem Punkt schneiden, d.h. wir suchen das a, so dass sich die beiden Geraden in einem Punkt schneiden.

1. Lösungsmöglichkeit

Um einen möglichen Schnittpunkt der beiden Geraden zu erhalten, setzen wir sie zunächst mal gleich:

$(\begin{matrix} a \\ -21 \\ 5 \end{matrix}) + s \cdot (\begin{matrix} 5 \\ 5 \\ -2 \end{matrix})$ = $(\begin{matrix} 22 \\ 29 \\ 10 \end{matrix}) + t \cdot (\begin{matrix} 4 \\ 5 \\ 3 \end{matrix})$

Als Gleichungssystem geschrieben:

$\begin{matrix} a & +5 s & = & 22 & +4 t & | -4 t \\ -21 & +5 s & = & 29 & +5 t & | -5 t +21 \\ 5 & -2 s & = & 10 & +3 t & | -3 t -5 \end{matrix}$

Wir haben also 3 Gleichungen und insgesamt 3 Variablen: a, s und t und können somit das LGS eindeutig lösen:

\begin{matrix} a & + 5 s & - 4 t & = & 22 & (I) \\ + 5 s & - 5 t & = & 50 & (II) \\ - 2 s & - 3 t & = & 5 & (III) \end{matrix}

\begin{matrix} 1 a & + 5 s & - 4 t & = & + 22 & (I) \\ 0 a & + 5 s & - 5 t & = & + 50 & (II) \\ 0 a & - 2 s & - 3 t & = & + 5 & (III) \end{matrix}

\begin{matrix} a & + 5 s & - 4 t & = & 22 & (I) \\ + 5 s & - 5 t & = & 50 & (II) \\ - 2 s & - 3 t & = & 5 & (III) \end{matrix}

langsame Rechnung einblenden $2$ ·(II) + $5$ ·(III)

\begin{matrix} 1 a & 5 s & - 4 t & = & 22 & (I) \\ 5 s & - 5 t & = & 50 & (II) \\ + (10 - 10) s & + (- 10 - 15) t & = & (100 + 25) & (III) \end{matrix}

\begin{matrix} a & + 5 s & - 4 t & = & 22 & (I) \\ + 5 s & - 5 t & = & 50 & (II) \\ - 25 t & = & 125 & (III) \end{matrix}

Zeile (III):

\begin{matrix} - 25 t & = & 125 \end{matrix}

t = $- 5$

eingesetzt in Zeile (II):

\begin{matrix} + 5 s & - 5 \cdot (- 5) & = & 50 \end{matrix}

| -

25

5

s =

25

| : 5

s = $5$

eingesetzt in Zeile (I):

\begin{matrix} a & + 5 \cdot (5) & - 4 \cdot (- 5) & = & 22 \end{matrix}

| -

45

1

a =

- 23

| : 1

a = $- 23$

$L = {(- 23 | 5 | - 5)}$

Für a = $- 23$ schneiden sich also die beiden Geraden g_{$- 23$}: $\vec{x} =$ $(\begin{matrix} -23 \\ -21 \\ 5 \end{matrix}) + t \cdot (\begin{matrix} 5 \\ 5 \\ -2 \end{matrix})$ und h.
Als Probe setzen wir noch die Parameter s = 5 in g_{$- 23$}: und t = -5 in g ein:

$\vec{OS}$ = $(\begin{matrix} -23 \\ -21 \\ 5 \end{matrix}) + 5 \cdot (\begin{matrix} 5 \\ 5 \\ -2 \end{matrix})$ = $(\begin{matrix} 2 \\ 4 \\ -5 \end{matrix})$

$\vec{OS}$ = $(\begin{matrix} 22 \\ 29 \\ 10 \end{matrix}) - 5 \cdot (\begin{matrix} 4 \\ 5 \\ 3 \end{matrix})$ = $(\begin{matrix} 2 \\ 4 \\ -5 \end{matrix})$

Für a = $- 23$ schneiden sich also die beiden Geraden im Punkt $(2 | 4 | -5)$ .

fehlende Gerade einer Ebene

Beispiel:

Gegeben ist eine Geradenschar g_a durch $\vec{x} =$ $(\begin{matrix} -4 \\ -5 \\ 3 \end{matrix}) + t \cdot (\begin{matrix} 1 \\ 3 \\ a \end{matrix})$ .

Bestimme eine Ebene E, in der alle Geraden der Geradenschar g_a liegen und gib eine Gerade h an, die in dieser Ebene liegt und durch den Punkt $(-4 | -5 | 3)$ geht, die aber nicht zur Geradenschar g_a gehört.

Lösung einblenden

Alle Geraden der Schar haben den selben Aufpunkt, haben aber verschiedene Richtungsvektoren.

Wenn es einen Ebene gibt, in der alle Geraden liegen, so muss diese einen Normalenvektor besitzen, der orthogonal zu all diesen verschiedenen Richtungsvektoren ist.

Es muss also gelten: $(\begin{matrix} 1 \\ 3 \\ a \end{matrix})$ ⋅ $(\begin{matrix} n_{1} \\ n_{2} \\ n_{3} \end{matrix})$ =0

Da in der x₃-Koordinate des Richtungsvektors der Parameter jeden beliebigen Wert annehmen kann, muss der n₃-Wert des Normalenvektor =0 sein, so hat das Skalarprodukt für jedes verschiedene a den selben Wert. Um diesen Wert jetzt auch noch auf 0 zu bekommen, müssen wir einfach die anderen beiden Koordinaten vertauschen und bei einem noch das Vorzeichen wechseln.

Also $\vec{n}$ = $(\begin{matrix} -3 \\ 1 \\ 0 \end{matrix})$ , denn $(\begin{matrix} 1 \\ 3 \\ a \end{matrix})$ ⋅ $(\begin{matrix} -3 \\ 1 \\ 0 \end{matrix})$ =0, für jedes beliebige a.

Die gesuchte gemeinsame Ebene hat also die Form: $-3 x_{1} + x_{2} = d$ .

Jetzt brauchen wir nur noch einen Punkt dieser Ebene, um das Absolutglied d noch zu bestimmen. Dafür können wir ja den Aufpunkt von g_a $(-4 | -5 | 3)$ nehmen. Denn dieser ist ja für jedes a gleich, also auf jeder Geraden g_a und somit auch auf der gesuchten gemeinsamen Ebene E.

Eingesetzt in die bisherige Ebenengleichung erhalten wir $(-3) \cdot (-4) + 1 \cdot (-5) + 0 \cdot 3$ =7=d

Die gesuchte gemeinsame Ebenen hat also die Gleichung: $-3 x_{1} + x_{2} = 7$

Gerade h in E, die nicht zur Schar g_a gehört:

Die Richtungsvektor der gesuchten Gerade h muss natürlich auch othogonal zum Normalenvektor $\vec{n}$ = $(\begin{matrix} 3 \\ -1 \\ 0 \end{matrix})$ sein.

Dies gilt aber für den Vektor $(\begin{matrix} 0 \\ 0 \\ 1 \end{matrix})$ , denn $(\begin{matrix} 0 \\ 0 \\ 1 \end{matrix})$ ⋅ $(\begin{matrix} -3 \\ 1 \\ 0 \end{matrix})$ =0.

Man kann die Richtung des Vektors $(\begin{matrix} 0 \\ 0 \\ 1 \end{matrix})$ als Grenzfall des allgemeinen Richtungsvektors der Geradenschar $(\begin{matrix} 1 \\ 3 \\ a \end{matrix})$ für a → ∞ sehen, die aber nie erreicht wird.

Die gesuchte Gerade h hat somit die Gleichung: $\vec{x} =$ $(\begin{matrix} -4 \\ -5 \\ 3 \end{matrix}) + t \cdot (\begin{matrix} 0 \\ 0 \\ 1 \end{matrix})$

kleinster Abstand zum Ursprung

Beispiel:

Gegeben ist eine Geradenschar g_a durch $\vec{x} =$ $(\begin{matrix} -3 \\ a \\ -4 \end{matrix}) + t \cdot (\begin{matrix} -1 \\ -5 \\ 2 \end{matrix})$ .

Für welchen Wert von a, hat die Gerade g_a den kleinstmöglchen Abstand zum Ursprung ?

Lösung einblenden

Um den kleinstmöglichen Abstand überhaupt abschätzen zu können, betrachten wir zuerst die Menge aller Punkte von allen Geraden der Schar: Das ist eine Ebene und deren Abstand vom Ursprung ist auch der (theoretisch) kleinstmögliche einer Geraden der Geradenschar.

1. Ebene bestimmen, in der alle Geraden liegen

Die Gerade lässt sich auch anders schreiben:
$\vec{x} =$ $(\begin{matrix} -3 \\ a \\ -4 \end{matrix}) + t \cdot (\begin{matrix} -1 \\ -5 \\ 2 \end{matrix})$ = $(\begin{matrix} -3 \\ 0 \\ -4 \end{matrix})$ + $(\begin{matrix} 0 \\ a \\ 0 \end{matrix})$ + t ⋅ $(\begin{matrix} -1 \\ -5 \\ 2 \end{matrix})$ = $(\begin{matrix} -3 \\ 0 \\ -4 \end{matrix})$ + a ⋅ $(\begin{matrix} 0 \\ 1 \\ 0 \end{matrix})$ + t ⋅ $(\begin{matrix} -1 \\ -5 \\ 2 \end{matrix})$

Durch Einsetzen der verschiedenen Werte für a und t erhält man alle Punkte, die auf einer der Geraden g_a liegen. Man sieht, dass diese Punktmenge eine Ebene ist, die hier bereits in Parameterform vorliegt.

Der Normalenvektor $\vec{n}$ dieser Ebene muss also orthogonal zu $(\begin{matrix} 0 \\ 1 \\ 0 \end{matrix})$ und $(\begin{matrix} -1 \\ -5 \\ 2 \end{matrix})$ sein.

Wenn er aber orthogonal zu $(\begin{matrix} 0 \\ 1 \\ 0 \end{matrix})$ sein soll, so muss er die Form $(\begin{matrix} n1 \\ 0 \\ n3 \end{matrix})$ haben, damit $(\begin{matrix} n1 \\ 0 \\ n3 \end{matrix})$ ⋅ $(\begin{matrix} 0 \\ 1 \\ 0 \end{matrix})$ =0 gilt.

Damit $(\begin{matrix} n1 \\ 0 \\ n3 \end{matrix})$ auch noch orthogonal zu $(\begin{matrix} -1 \\ -5 \\ 2 \end{matrix})$ ist, muss jetzt ja nur noch die Einträge in der x₃- und der x₁-Koordinate nehmen und vertauschen und ein Vorzeichen umdrehen, also $\vec{n}$ = $(\begin{matrix} 2 \\ 0 \\ 1 \end{matrix})$ , so dass auch $(\begin{matrix} 2 \\ 0 \\ 1 \end{matrix})$ ⋅ $(\begin{matrix} -1 \\ -5 \\ 2 \end{matrix})$ =0 gilt.

Natürlich hätte man den Normalenvektor auch mit dem Vektorprodukt bestimmen können, statt nur scharf hinzusehen.

Unsere Ebenengleichung in Koordinatenform ist also $2 x_{1} + x_{3} = d$ .
Durch Einsetzen des Aufpunktes der Ebene A $(-3 | 0 | -4)$ erhält man d = $2 \cdot (-3) + 0 \cdot 0 + 1 \cdot (-4)$ = -10
also gilt:

E: $2 x_{1} + x_{3} = -10$

2. Lotfußpunkt von E zum Ursprung

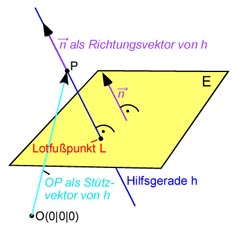Der Lotfußpunkt der Ebene E zum Ursprung ist der Punkt der Ebene E mit dem kleinsten Abstand zum Ursprung. Wenn wir diesen haben und dann eine Gerade der Schar, die durch diesen Punkt gehen würde, wären wir am Ziel.

Dazu stellen wir eine Hilfsgerade mit dem Normalenvektor von E als Richtungsvektor und dem Ursprung als Stützpunkt auf:
h: $\vec{x} =$ $(\begin{matrix} 0 \\ 0 \\ 0 \end{matrix}) + t \cdot (\begin{matrix} 2 \\ 0 \\ 1 \end{matrix})$

Diese schneiden wir mit der Ebene E:

Dazu setzen wir einfach den allgemeinen Geradenpunkt von h: $H_{t} (0 + 2 t | 0 + 0 t | 0 + 1 t)$ in die Ebene E ein und lösen nach t auf:

$2 \cdot 2 t + 0 \cdot 0 + 1 \cdot t$ = $- 10$

$2 \cdot 2 t + 0 \cdot 0 + 1 \cdot t$	=	$- 10$
$4 t + t$	=	$- 10$
$5 t$	=	$- 10$	\|: $5$
$t$	=	$- 2$

Den Lotfußpunkt als gesuchten Durchstoßpunkt erhalten wir, indem wir dieses t in die Geradengleichung bzw. in den allg. Geradenpunkt $H_{t} (0 + 2 t | 0 + 0 t | 0 + 1 t)$ einsetzen:

L $(-4 | 0 | -2)$

3. Parameter a bestimmen, so dass L auf g_a liegt

Da sich ja die Geraden g_a für die verschiedenen a praktisch über die ganze Ebene verteilen, müsste es doch auch eine Gerade geben, auf der dieser Lotfußpunkt liegt. Das zugehörige a versuchen wir zu bestimmen, in dem wir den Lotfußpunkt in die Geradengleichung einsetzen:

$(\begin{matrix} -4 \\ 0 \\ -2 \end{matrix})$ = $(\begin{matrix} -3 \\ a \\ -4 \end{matrix}) + t \cdot (\begin{matrix} -1 \\ -5 \\ 2 \end{matrix})$

-4 = -3-1⋅t=> -1⋅t = -1 also t = 1

0 = a-5⋅t

-2 = -4+2⋅t=> 2⋅t = 2 also t = 1

Setzen wir nun diese t = 1 in die 2-te Zeile ein, so erhalten wir:
0 = a -5, also a = 5

Also liegt der Lotfußpunkt L $(-4 | 0 | -2)$ auf der Geraden g₅ (mit t = 1). Da alle Geraden g_a in der Ebene liegen, kann kein Punkt einer anderen Geraden der Schar näher am Ursprung liegen als der Lotfußpunkt der Ebene L $(-4 | 0 | -2)$ . Folglich ist die Gerade g₅ (mit a=5) die Gerade der Schar mit dem kleinstmöglchen Abstand zum Ursprung.

Ebenenschar min. Abstand

Beispiel:

Gegeben ist eine Ebenenschar E_a durch E_a: $5 x_{1} + a x_{2} + x_{3} = 3a + 26$ .
Von den Punkten, die in jeder Ebene der Ebenenschar E_a liegen, gibt es einen mit dem kleinsten Abstand zum Ursprung.

Bestimme dessen Koordinaten.

Lösung einblenden

Die Punkte, die in jeder der Ebenenscharen liegen, bilden oft eine gemeinsame Gerade. Wenn es eine solche Geraden gibt, die in allen Ebenen der Schar liegt, so muss deren Richtungsvektor $(\begin{matrix} r_{1} \\ r_{2} \\ r_{3} \end{matrix})$ orthogonal zu allen Normalenvektoren der verschiedenen Ebenen der Schar sein, weil eben alle Vektoren einer Ebene immer orthogonal zum Normalenvektor der Ebene sind.

Es muss also gelten: $(\begin{matrix} r_{1} \\ r_{2} \\ r_{3} \end{matrix})$ ⋅ $(\begin{matrix} 5 \\ a \\ 1 \end{matrix})$ =0

Um das Ergebnis des Skalarprodukts unabhängig von a zu bekommen, setzen wir r₂ einfach mal =0. Für die anderen beiden Werte r₃ und r₁ nehmen wir einfach die jeweils andere Koordinate des Normalenvektors und drehen bei einem noch das Vorzeichen, so dass das Skalarprodukt auf jeden Fall Null ergibt.

Also : $(\begin{matrix} -1 \\ 0 \\ 5 \end{matrix})$ ⋅ $(\begin{matrix} 5 \\ a \\ 1 \end{matrix})$ =0. Der Richtungsvektor $\vec{r}$ = $(\begin{matrix} -1 \\ 0 \\ 5 \end{matrix})$ steht also senkrecht auf allen Normalenvektoren und ist damit in allen Ebenen E_a enthalten.

Jetzt brauchen wir noch einen Stützvektor der gemeinsamen Geraden, also den Ortsvektor zu einem Punkt, der in allen Ebenen E_a liegt, also einen Punkt, der die Ebenengleichung E_a: $5 x_{1} + a x_{2} + x_{3} = 3a + 26$ für jedes a erfüllt.

Da auf der rechten Seite der Ebenengleichung 3a + 26 steht, können die 3a auf der linken Seite nur durch Einsetzen von 3 für x₂ erreicht werden. Für die 26 gibt es mehrere Möglichkeiten, z.B. 0 für x₁ und 26 für x₃, weil 5⋅0 +1⋅26 = 26.

So erhalten wir also den Punkt $(0 | 3 | 26)$ , der auf jeder Ebene E_a liegt, denn eingesetzt in E_a erhalten wir: 3a + 26 = 3a + 26.

$(\begin{matrix} 0 \\ 3 \\ 26 \end{matrix})$ ist also unser gesuchter Stützvektor.

Die Gerade g: $\vec{x} =$ $(\begin{matrix} 0 \\ 3 \\ 26 \end{matrix}) + t \cdot (\begin{matrix} -1 \\ 0 \\ 5 \end{matrix})$ liegt also in jeder Ebene E_a.

(Zur Kontrolle kann man übrigends den allgemeinen Geradenpunkt der Lösungsgeraden wieder in die Ebenegleichung E_a einsetzen und es muss 0=0 herauskommen)

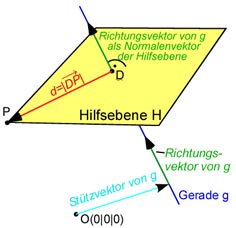Um den Geradenpunkt mit dem kleinsten Abstand zum Punkt $(0 | 0 | 0)$ zu bestimmen, bilden wir eine Hilfsebene, die orthogonal zu unserer Geraden $\vec{x} =$ $(\begin{matrix} 0 \\ 3 \\ 26 \end{matrix}) + t \cdot (\begin{matrix} -1 \\ 0 \\ 5 \end{matrix})$ ist und unseren Punkt P $(0 | 0 | 0)$ enthält.
Der Normalenvektor der Hilfsebene ist also der Richtungsvektor der Geraden, $(\begin{matrix} -1 \\ 0 \\ 5 \end{matrix})$ . Die Hilfsebene in der Koordinatenform hat somit die Form $- x_{1} + 5 x_{3} = d$ . Wenn man den Punkt $(0 | 0 | 0)$ darin einsetzt, erhält man d = $(-1) \cdot 0 + 0 \cdot 0 + 5 \cdot 0$ = 0.
Nun berechnen wir den Durchstoßpunkt der Geraden mit der Hilfsebene $- x_{1} + 5 x_{3} = 0$ .

Wir setzen einen allgemeinen Geradenpunkt der Geraden $G_{t} (0 - 1 t | 3 + 0 t | 26 + 5 t)$ in die Ebene ein und lösen nach t auf:

$- 1 \cdot (- t) + 0 \cdot 3 + 5 \cdot (26 + 5 t)$	=	0
$t + 130 + 25 t$	=	0
$26 t + 130$	=	0	\| $- 130$
$26 t$	=	$- 130$	\|: $26$
$t$	=	$- 5$

Den Durchstoßpunkt erhalten wir, indem wir dieses t in die Geradengleichung bzw. in den allg. Geradenpunkt $G_{t} (0 - 1 t | 3 + 0 t | 26 + 5 t)$ einsetzen.
=> D $(5 | 3 | 1)$ .

Der Verbindungsvektor vom Ursprung zu diesem Geradenpunkt, also der Ortvektor $(\begin{matrix} 5 \\ 3 \\ 1 \end{matrix})$ steht also orthogonal zur gemeinsamen Gerade der Ebenenschar: $(\begin{matrix} 5 \\ 3 \\ 1 \end{matrix})$ ⋅ $(\begin{matrix} -1 \\ 0 \\ 5 \end{matrix})$ =0

Damit ist der Punkt L $(5 | 3 | 1)$ der Punkt auf dieser Geraden mit der kürzesten Entfernung zum Ursprung.

Ebenenschar fester Abstand

Beispiel:

Gegeben ist eine Ebenenschar E_a durch E_a: $5 x_{1} + a x_{2} - 5 x_{3} = 8a + -20$ .
Von den Punkten, die in jeder Ebene der Ebenenschar E_a liegen, gibt es zwei Punkte mit dem Abstand 12 zum Ursprung.

Bestimme die Koordinaten von einem der beiden Punkte.

Lösung einblenden

Die Punkte, die in jeder der Ebenenscharen liegen, bilden oft eine gemeinsame Gerade. Wenn es eine solche Geraden gibt, die in allen Ebenen der Schar liegt, so muss deren Richtungsvektor $(\begin{matrix} r_{1} \\ r_{2} \\ r_{3} \end{matrix})$ orthogonal zu allen Normalenvektoren der verschiedenen Ebenen der Schar sein, weil eben alle Vektoren einer Ebene immer orthogonal zum Normalenvektor der Ebene sind.

Es muss also gelten: $(\begin{matrix} r_{1} \\ r_{2} \\ r_{3} \end{matrix})$ ⋅ $(\begin{matrix} 5 \\ a \\ -5 \end{matrix})$ =0

Um das Ergebnis des Skalarprodukts unabhängig von a zu bekommen, setzen wir r₂ einfach mal =0. Für die anderen beiden Werte r₃ und r₁ nehmen wir einfach die jeweils andere Koordinate des Normalenvektors und drehen bei einem noch das Vorzeichen, so dass das Skalarprodukt auf jeden Fall Null ergibt.

Also : $(\begin{matrix} 5 \\ 0 \\ 5 \end{matrix})$ ⋅ $(\begin{matrix} 5 \\ a \\ -5 \end{matrix})$ =0. Der Richtungsvektor $\vec{r}$ = $(\begin{matrix} 5 \\ 0 \\ 5 \end{matrix})$ oder $(\begin{matrix} 1 \\ 0 \\ 1 \end{matrix})$ steht also senkrecht auf allen Normalenvektoren und ist damit in allen Ebenen E_a enthalten.

Jetzt brauchen wir noch einen Stützvektor der gemeinsamen Geraden, also den Ortsvektor zu einem Punkt, der in allen Ebenen E_a liegt, also einen Punkt, der die Ebenengleichung E_a: $5 x_{1} + a x_{2} - 5 x_{3} = 8a + -20$ für jedes a erfüllt.

Da auf der rechten Seite der Ebenengleichung 8a + -20 steht, können die 8a auf der linken Seite nur durch Einsetzen von 8 für x₂ erreicht werden. Für die -20 gibt es mehrere Möglichkeiten, z.B. 0 für x₁ und 4 für x₃, weil 5⋅0 -5⋅4 = -20.

So erhalten wir also den Punkt $(0 | 8 | 4)$ , der auf jeder Ebene E_a liegt, denn eingesetzt in E_a erhalten wir: 8a + -20 = 8a + -20.

$(\begin{matrix} 0 \\ 8 \\ 4 \end{matrix})$ ist also unser gesuchter Stützvektor.

Die Gerade g: $\vec{x} =$ $(\begin{matrix} 0 \\ 8 \\ 4 \end{matrix}) + t \cdot (\begin{matrix} 1 \\ 0 \\ 1 \end{matrix})$ liegt also in jeder Ebene E_a.

(Zur Kontrolle kann man übrigends den allgemeinen Geradenpunkt der Lösungsgeraden wieder in die Ebenegleichung E_a einsetzen und es muss 0=0 herauskommen)

Der gesuchte Punkt muss also auf dieser Geraden liegen, folglich können wir ihn als allgemeinen Geradenpunkt $G_{t} (0 + 1 t | 8 + 0 t | 4 + 1 t)$ darstellen.
Der Abstand zwischen dem allgemeinen Geradenpunkt G_t und dem Punkt O ist die Länge des Vektors $\vec{OGt}$ ,
also d=| $\vec{OGt}$ | = $| (\begin{matrix} 0 + 1 t \\ 8 + 0 t \\ 4 + 1 t \end{matrix}) |$ = $\sqrt{{(0 + t)}^{2} + {(8 + 0)}^{2} + {(4 + t)}^{2}}$ = 12 |²

{(0 + t)}^{2} + {(8 + 0)}^{2} + {(4 + t)}^{2}

= 144

t^{2} + 64 + (t^{2} + 8 t + 16)

= 144

2 t^{2} + 8 t + 80

=

144

|

- 144

2 t^{2} + 8 t - 64

= 0 |:2

$t^{2} + 4 t - 32$ = 0

eingesetzt in die Mitternachtsformel (a-b-c-Formel):

t_1,2 = $\frac{- 4 \pm \sqrt{4^{2} - 4 \cdot 1 \cdot (- 32)}}{2 \cdot 1}$

t_1,2 = $\frac{- 4 \pm \sqrt{16 + 128}}{2}$

t_1,2 = $\frac{- 4 \pm \sqrt{144}}{2}$

t₁ = $\frac{- 4 + \sqrt{144}}{2}$ = $\frac{- 4+12}{2}$ = $\frac{8}{2}$ = $4$

t₂ = $\frac{- 4 - \sqrt{144}}{2}$ = $\frac{- 4-12}{2}$ = $\frac{- 16}{2}$ = $- 8$

Da nur einer der beiden Punkte gesucht ist, setzen wir nur die Lösung t = -8 wieder in die Gerade, bzw. in den allgemeinen Geradenpunkt ein:

$(\begin{matrix} 0 \\ 8 \\ 4 \end{matrix}) - 8 \cdot (\begin{matrix} 1 \\ 0 \\ 1 \end{matrix})$ = $(\begin{matrix} -8 \\ 8 \\ -4 \end{matrix})$

Der Punkt P $(-8 | 8 | -4)$ liegt also auf der gemeinsamen Geraden aller Ebenen der Schar E_a und hat vom Ursprung die Entfernung $\sqrt{{(-8)}^{2} + 8^{2} + {(-4)}^{2}} = \sqrt{144} = 12$ .

orthogonale Ebenen in Schar

Beispiel:

Gegeben ist die Ebenenschar E_a: $5 x_{1} + a x_{2} + 5 x_{3} = -3$ , a ∈ ℝ

a) Für welches a ist ist E_a orthogonal zu E ₂ ?

b) Bestimme die Ebene E_c der Ebenenschar E_a, für die es keine orthogonale Ebene aus der Schar gibt.

Lösung einblenden

a) Damit sich die beiden Ebenen orthogonal schneiden, müssen ihre Normalenvektoren orthogonal sein,
d.h. deren Skalarprodukt muss =0 sein: $(\begin{matrix} 5 \\ a \\ 5 \end{matrix})$ ⋅ $(\begin{matrix} 5 \\ 2 \\ 5 \end{matrix})$ = $5 \cdot 5 + a \cdot 2 + 5 \cdot 5$ = 0.

$5 \cdot 5 + a \cdot 2 + 5 \cdot 5$	=	0
$25 + 2 a + 25$	=	0
$2 a + 50$	=	0	\| $- 50$
$2 a$	=	$- 50$	\|: $2$
$a$	=	$- 25$

Somit ist E_-25 orthogonal zu E₂: $(\begin{matrix} 5 \\ -25 \\ 5 \end{matrix})$ ∘ $(\begin{matrix} 5 \\ 2 \\ 5 \end{matrix})$ = $5 \cdot 5 + (-25) \cdot 2 + 5 \cdot 5 = 25 -50 +25 = 0$

b) Egal zu welcher E_c wir eine orthogonale Ebene suchen, funktioniert die Rechnung (fast) immer gleich wie bei E₂:
Man erhält immer das gesuchte a in dem man die -50 durch das gegebene c (oben die 2) teilt, außer eben wenn dieses c = 0 ist:

Dann ist das Skalarprodukt $(\begin{matrix} 5 \\ 0 \\ 5 \end{matrix})$ ⋅ $(\begin{matrix} 5 \\ a \\ 5 \end{matrix})$ = 50 immer ≠ 0, egal welchen Wert a annimmt.

Die gesuchte Ebene ist somit $5 x_{1} + 5 x_{3} = -3$

Maximaler Abstand Pkt-Ebene

Beispiel:

Für alle a ∈ ℝ sind die Ebenen E_a: $-12 x_{1} + 9 x_{2} + a x_{3} = 15$ und F_a: $-12 x_{1} + 9 x_{2} + a x_{3} = -39$ parallel.

Bestimme den größtmöglichen Abstand zwischen E_a und F_a.

Lösung einblenden

Den Abstand zwischen zwei parallelen Ebenen berechnen wir am einfachsten als Abstand eines beliebigen Punktes der einen Ebene zur anderen Ebene.

Dazu berechnen wir erstmal einen Spurpunkt von F_a. Da der Koeffizient vor dem x₁ keinen Parameter a enthält, bietet sich S₁ an:

-12x₁ = -39, somit ist x₁ = $\frac{39}{12}$

Als Abstand zwischen E_a und F_a berechnen wir also den Abstand des Spurpunkts S_F $(\frac{39}{12} | 0 | 0)$ von der Ebene E_a.

Nach der Hesse'schen Normalenform muss gelten:

d(E_a,F_a)= d(S_F, E_a) = $\frac{| - 12 \cdot \frac{39}{12} - 15 |}{\sqrt{{(- 12)}^{2} + 9^{2} + {(a)}^{2}}}$ = $\frac{| - 39 - 15 |}{\sqrt{{(- 12)}^{2} + 9^{2} + {(a)}^{2}}}$ = $\frac{54}{\sqrt{a^{2} + 225}}$

Da der Zähler konstant ist, ändert sich die Größe des Abstands nur durch das a im Nenner.

Für einen maximalen Wert, muss der Nenner minimal werden.

Man sieht hier recht schnell, dass dieser minimale Nenner bei a=0 ist, da ja immer a²≥0 gilt.

Der maximale Abstand ist dann d(E_a,F_a)= d(S_F, E_a) = $\frac{| 54 |}{\sqrt{225}}$ = $\frac{| 54 |}{15}$ = 3,6

Minimaler Schnittwinkel

Beispiel:

Gegeben ist für alle a∈ℝ die Geradenschar g_a durch g_a: $\vec{x} =$ $(\begin{matrix} 4 \\ -2 \\ -4 \end{matrix}) + t \cdot (\begin{matrix} 6 \\ -7 \\ a \end{matrix})$ sowie die Ebene E: $2 x_{1} + 6 x_{2} = -4$ .

Dabei sind nicht alle Werte für den Schnittwinkel zwischen g_a und E möglich. Berechne den maximalen bzw. minimalen Schnittwinkel zwischen g_a und E.

Lösung einblenden

Wir berechnen den Schnittwinkel zwischen g_a und Ebene E: $2 x_{1} + 6 x_{2} = -4$ in Abhängigkeit vom Parameter a mit der Formel:

sin(γ) = $\frac{| (\begin{matrix} 6 \\ -7 \\ a \end{matrix}) \circ (\begin{matrix} 2 \\ 6 \\ 0 \end{matrix}) |}{| (\begin{matrix} 6 \\ -7 \\ a \end{matrix}) | \cdot | (\begin{matrix} 2 \\ 6 \\ 0 \end{matrix}) |}$

= $\frac{| 6 \cdot 2 + (-7) \cdot 6 + a \cdot 0 |}{\sqrt{6^{2} + {(-7)}^{2} + a^{2}} \cdot \sqrt{2^{2} + 6^{2} + 0^{2}}}$

= $\frac{| 30 |}{\sqrt{36 + 49 + a^{2}} \cdot \sqrt{4 + 36 + 0}}$

= $\frac{30}{\sqrt{a^{2} + 85} \cdot \sqrt{40}}$

Da im Nenner nur positive Zahlen (Wurzeln) sind, nimmt der Nenner bei a = 0 seinen kleinsten Wert und der ganze Bruchterm somit mit $\frac{30}{\sqrt{85} \cdot \sqrt{40}}$ = $\frac{30}{\sqrt{3 400}}$ ≈ 0.514 seinen größtmöglichen Wert an, während für a → ±∞ der Nenner beliebig groß wird und somit der ganze Bruchterm gegen 0 strebt.

Der sin(γ) kann also nur Werte im Intervall ]0 ; 0,514] annehmen.

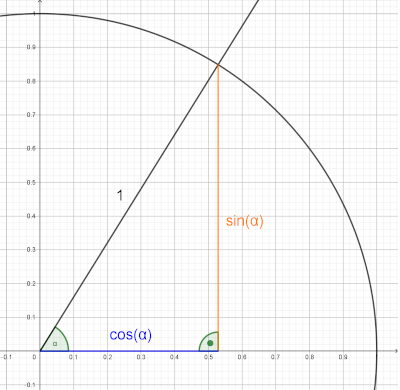Der sin(γ) nimmt für $\frac{30}{\sqrt{3 400}}$ ≈ 0.514 also seinen größten Wert an. Das kann man auf verschiedene Weisen begründen:

Trigonometrisch am Einheitskreis: Je größer der Winkel γ wird, desto größer wird der sin(γ)-Wert
Geometrisch: Wenn das Skalarprodukt und damit der sin(γ)=0 ist, sind ja g_a und E parallel und mit größer werdendem sin(γ) wird Winkel zunehmend größer.

Der maximale Schnittwinkel ist somit bei γ = arcsin(0,514) ≈ 31°.

Aufgabenbeispiele von Parameteraufgaben

orthogonale Vektoren

gemeinsame Ebene einer Geradenschar1

gemeinsame Gerade einer Ebenenschar

gegebener Abstand zu Punkt

Gerade schneidet x-Achse

gegebener Steigungswinkel

Parameter für Schnittpunkt wählen

1. Lösungsmöglichkeit

fehlende Gerade einer Ebene

Gerade h in E, die nicht zur Schar ga gehört:

kleinster Abstand zum Ursprung

1. Ebene bestimmen, in der alle Geraden liegen

2. Lotfußpunkt von E zum Ursprung

3. Parameter a bestimmen, so dass L auf ga liegt

Ebenenschar min. Abstand

Ebenenschar fester Abstand

orthogonale Ebenen in Schar

Maximaler Abstand Pkt-Ebene

Minimaler Schnittwinkel

Gerade h in E, die nicht zur Schar g_a gehört:

3. Parameter a bestimmen, so dass L auf g_a liegt