Aufgabenbeispiele von 3D-KoSy
Durch Aktualisieren des Browsers (z.B. mit Taste F5) kann man neue Beispielaufgaben sehen
Punkte in einem Quader bestimmen
Beispiel:
Im Schaubild rechts ist ein Quader in ein 3-dimensionales Koordinatensystem eingezeichnet. Die Quaderseiten sind parallel zu den Koordinatenebenen. Der Punkt D hat die Koordinaten D. Der Quader ist (in x1-Richtung) 3 Einheiten tief, 3 Einheiten breit und 3 Einheiten hoch.
Gib die Koordinaten der Punkte H und A an.
Da ja D auf der unteren Quaderfläche liegt, müssen auch die Punkte A, C und B als x3-Koordinate 2 haben, weil sie ja auch auf der unteren Quaderfläche liegen.
Da die Kante DA parallel zur x1-Achse liegt, muss A auch die gleiche x2-Koordinate wie D haben. Die x1-Koordinate muss wegen der gegebenen Tiefe 3 Einheiten Abstand in x1-Richtung haben, somit gilt A.
Da die Kante DC parallel zur x2-Achse liegt, muss C auch die gleiche x1-Koordinate wie D haben. Die x2-Koordinate muss wegen der gegebenen Breite 3 Einheiten Abstand in x2-Richtung haben, somit gilt C.
Mit den gleichen Überlegungen kann man sehen, dass B die gleiche x1-Koordinate wie A und die gleiche x2-Koordinate wie C haben muss, somit gilt: B.
Die anderen 4 Punkte H, G, E und F liegen ja genau über D, A, C und B und haben somit jeweils die gleichen x1- und x2-Koordinaten und unterscheiden sich nur in der x3-Koordinate, die eben um 3 Einheiten größer sein muss. Somit gilt: H, G, E, F.
Koordinaten im Würfel finden
Beispiel:
Im Schaubild rechts ist ein Würfel in ein 3-dimensionales Koordinatensystem eingezeichnet. Die Würfelseiten sind parallel zu den Koordinatenebenen. Der Punkt C hat die Koordinaten C, der Punkt E hat die Koordinaten E.
Gib die Koordinaten der Punkte D und G an.
C und E unterscheiden sich in der x1-Koordinate um 3, somit ist die Kantenlänge des Würfels 3.
Da ja C auf der unteren Quaderfläche liegt, müssen auch die Punkte B, D und A als x3-Koordinate 0 haben, weil sie ja auch auf der unteren Quaderfläche liegen.
Da die Kante CB parallel zur x1-Achse liegt, muss B auch die gleiche x2-Koordinate wie C haben. Die x1-Koordinate muss wegen der gegebenen Tiefe 3 Einheiten Abstand in x1-Richtung haben, somit gilt B.
Da die Kante CD parallel zur x2-Achse liegt, muss D auch die gleiche x1-Koordinate wie C haben. Die x2-Koordinate muss wegen der gegebenen Breite 3 Einheiten Abstand in x2-Richtung haben, somit gilt D.
Mit den gleichen Überlegungen kann man sehen, dass A die gleiche x1-Koordinate wie B und die gleiche x2-Koordinate wie D haben muss, somit gilt: A.
Die anderen 4 Punkte G, F, H und E liegen ja genau über C, B, D und A und haben somit jeweils die gleichen x1- und x2-Koordinaten und unterscheiden sich nur in der x3-Koordinate, die eben um 3 Einheiten größer sein muss. Somit gilt: G, F, H, E.
A, B und Mittelpunkt davon
Beispiel:
Gegeben sind die Punkte A, B und der Mittelpunkt M der Strecke AB. Bestimme die Koordinaten von A.
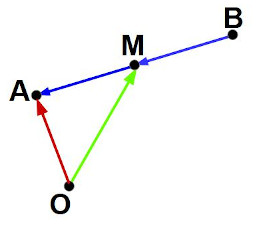 Wir sehen in der Skizze, dass der Verbindungsvektor von M zu A der gleiche ist wie der von B zu M, also =
= . Wir müssen also zum Ortsvektor von M addieren, um den Ortsvektor von A zu erhalten:
Wir sehen in der Skizze, dass der Verbindungsvektor von M zu A der gleiche ist wie der von B zu M, also =
= . Wir müssen also zum Ortsvektor von M addieren, um den Ortsvektor von A zu erhalten:
Die Koordinaten des gesuchten Punkts sind somit A.
Diagonalenschnittpkt Parallelogramm
Beispiel:
Berechne den Diagonalenschnittpunkt des Parallelogramms ABCD mit A, B, C und D.
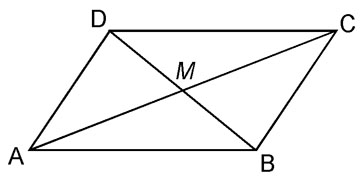 Im Parallelogramm halbieren sich die Diagonalen (Gegenüberliegende Teildreiecke sind kongruent
wegen einer gemeinsamen Seitenlänge und zwei gleichen (Wechsel-)Winkeln). Wir müssen also nur den Mittelpunkt
einer Diagonalen berechnen!
Im Parallelogramm halbieren sich die Diagonalen (Gegenüberliegende Teildreiecke sind kongruent
wegen einer gemeinsamen Seitenlänge und zwei gleichen (Wechsel-)Winkeln). Wir müssen also nur den Mittelpunkt
einer Diagonalen berechnen!
Mittelpunkte im Quader bestimmen
Beispiel:
Im Schaubild rechts ist ein Quader in ein 3-dimensionales Koordinatensystem eingezeichnet. Die Quaderflächen sind parallel zu den Koordinatenebenen. A, B, D und E sind Eckpunkte des Quaders.
M ist der Kantenmittelpunkt der Kante CG. Gib die Koordinaten von M an.
Da ja A, B und D auf der unteren Quaderfläche liegen und die Quaderflächen parallel zu den Koordinatenebenen liegen, muss auch der Punkt C als x3-Koordinate -2 haben, weil C ja auch auf der unteren Quaderfläche liegt.
Da die Kante BC parallel zur x1-Achse liegt, muss C auch die gleiche x2-Koordinate wie B haben und da die Kante CD parallel zur x2-Achse liegt, muss C die gleiche x1-Koordinate wie D haben. Somit gilt C.
Die anderen 4 Punkte E, F, G und h liegen ja genau über A, B, C und D und haben somit jeweils die gleichen x1- und x2-Koordinaten und unterscheiden sich nur in der x3-Koordinate. Da auch die Deckelfläche des Quaders parallel zur x1-x2-Ebnene liegt, müssen alle Punkte dieser Deckelfläche die selbe x3-Koordinate haben. Und da E als x3-Koordinate 1 hat, gilt: F, G, H.
Jetzt müssen wir nur noch den Mittelpunkt der Kante CG berechnen:
Den Mittelpunkt zwischen zwei Punkten kann man einfach berechnen, indem man in jede Koordinate den Mittelwert der beiden Werte in der jeweiligen Koordinate setzt:
.
Pyramidenberechnungen
Beispiel:
Im Schaubild rechts ist eine gerade Pyramide mit quadratischer Grundfläche in ein 3-dimensionales Koordinatensystem eingezeichnet. Die Grundfläche der Pyramide ist parallel zur x1-x2-Ebene. Der Punkt C hat die Koordinaten C, der Punkt D hat die Koordinaten D. Die Höhe der Pyramide beträgt 4 Einheiten.
Gib die Koordinaten der Spitze S an und berechne die Länge einer der Pyramidenkanten.
Da die Pyramide gerade ist, liegt die Spitze genau über dem Diagonalenschnittpunkt der Grundfläche der Pyramide. Diesen Diagonalenschnittpunkt können wir einfach als Mittelpunkt zweier gegenüberliegenden Punkte der Grundfläche berechen. Dazu brauchen wir aber noch mindestens einen weiteren Punkt der Grundfläche:
Der Punkt A muss natürlich auch als x3-Koordinate den Wert -3 haben, da ja die Grundfläche parallel zur x1-x2-Ebene ist, außerdem muss er die gleiche x2-Koordinate wie D haben. Da C und D den Abstand 6 haben, muss die x1-Koordinate von A auch um 6 größer sein, somit gilt: A .
Jetzt können wir den Mittelpunkt von C und A berechnen:
M.
Dieser Mittelpunkt M liegt nun am Fuß der Höhe h, die ja 4 Einheiten hoch ist. Somit muss die Spitze S der Pyramide die gleichen x1- und x2-Koordinaten wie M haben, allerdings einen um 4 größeren x3-Wert, also S.
Aufgrund der Symmetrie sind alle 4 Kanten der Pyramide gleich lang. Wenn wir das Dreieck CMS anschauen, erkennen wir, dass es in M einen rechten Winkel hat und wir somit den Satz des Pythagoras anwenden können: 2 = 2 + 2
Wir brauchen also noch die Strecke CM, diese ist aber ja gerade die Hälfte der Strecke CA
= =
d=|| = =
Jetzt können wir die Strecke CM =
=
=
=
Somit gilt für die gesuchte Kantenlänge:
Pyramide rückwärts
Beispiel:
Im Schaubild rechts ist eine gerade Pyramide mit quadratischer Grundfläche in ein 3-dimensionales Koordinatensystem eingezeichnet. Die Grundfläche der Pyramide ist parallel zur x1-x2-Ebene. Der Punkt A hat die Koordinaten A
Gib die Koordinaten der Spitze S an.
Da die Pyramide gerade ist, liegt die Spitze genau über dem Diagonalenschnittpunkt der Grundfläche der Pyramide. Diesen Diagonalenschnittpunkt können wir einfach als Mittelpunkt zweier gegenüberliegenden Punkte der Grundfläche berechnen. Dazu brauchen wir aber noch mindestens einen weiteren Punkt der Grundfläche:
Der Punkt C muss natürlich auch als x3-Koordinate den Wert -3 haben, da ja die Grundfläche
parallel zur x1-x2-Ebene ist, außerdem muss er die gleiche x2-Koordinate wie B haben.
Da A und B den Abstand 6 haben, muss die x1-Koordinate von
C auch um 6 kleiner sein, somit gilt: C
Jetzt können wir den Mittelpunkt von A und C berechnen:
M.
Dieser Mittelpunkt M liegt nun am Fuß der Höhe h. Deren Länge kennen wir zwar noch nicht, aber wir können sie über das gegebene Volumen berechnen:
Für das Volumen einer Pyramide gilt: V =
Und weil die Grundfläche G ein Quadrat mit Seitenlänge 6 ist, gilt:
4 = h
Die Höhe der Pyramide ist also h = 4
Die Spitze S der Pyramide muss also die gleichen x1- und x2-Koordinaten wie M haben, allerdings einen um 4 größeren
x3-Wert,
also S
Punkt an Achsenebene spiegeln
Beispiel:
Der Punkt
Berechne den Bildpunkt P'!
Die x1-x3-Ebene hat ja den Normalenvektor
Beide Punkte müssen ja aber den gleichen Abstand von der x1-x3-Ebene (x2=0) haben, also muss die
x2-Koordinate von P' direkt "gegenüber" von der von P sein. Somit gilt für den gespiegelten Bildpunkt P'
Objekte auf Koordinaten-Ebenen
Beispiel:
Gib zwei Punkte A und B an, die in der x1-x2-Ebene liegen und den Abstand 2 haben. Außerdem soll die Strecke AB parallel zur x1-Achse sein'!
Wenn die beiden Punkte in der x1-x2-Ebene liegen, muss die x3-Koordinate jeweils = 0 sein, das heißt beim ersten Punkt A
kann man alles außer der x3-Koordinate frei wählen, z.B. A
Da die Strecke AB parallel zur x1-Achse sein muss, sollte auch noch die x2-Koordinate bei A und B gleich sein, also gilt:
B
Um auf den Abstand 2 zwischen A und B zu kommen, müssen sich nun also die x1-Koordinaten bei A und B um 2 unterscheiden. Also
wäre beispielweise B
Punkte auf Koordinatenachse bestimmen
Beispiel:
Gib zwei Punkte A und B an, die auf der x3-Achse liegen und den Abstand 4 haben.
Wenn die beiden Punkte auf der x3-Achse liegen, müssen die x1-Koordinate und die x2-Koordinate
jeweils = 0 sein, das heißt beim ersten Punkt A kann man nur die x3-Koordinate frei wählen, z.B. A
Da auch bei B die x1-Koordinate und die x2-Koordinate =0 sein müssen, und der Abstand zu A 4 betragen soll,
muss eben die x3-Koordinate um 4 kleiner oder größer als bei A sein. Somit wäre beispielweise
B

