Pestalozzi Gymnasium Biberach EduRandomtasks

Normalenvektor ohne Kreuzprodukt

Beispiel:

Finde einen Vektor, der sowohl zu $\vec{u}$ = $(\begin{matrix} -1 \\ 4 \\ 0 \end{matrix})$ als auch zu $\vec{v}$ = $(\begin{matrix} 5 \\ -6 \\ -7 \end{matrix})$ orthogonal ist (der Nullvektor ist nicht erlaubt).

Lösung einblenden

Weil beim Vektor $(\begin{matrix} -1 \\ 4 \\ 0 \end{matrix})$ in der x₃-Koordinate eine 0 steht, wäre ja der Vektor $(\begin{matrix} -4 \\ -1 \\ t \end{matrix})$ für jedes t orthogonal zu $(\begin{matrix} -1 \\ 4 \\ 0 \end{matrix})$ , denn $(\begin{matrix} -1 \\ 4 \\ 0 \end{matrix})$ ∘ $(\begin{matrix} -4 \\ -1 \\ t \end{matrix})$ = $(-1) \cdot (-4) + 4 \cdot (-1) + 0 \cdot t = 4 -4 +0 = 0$ .

Nun müssen wir noch das t so bestimmen, dass auch das Skalarprodukt mit dem Vektor $(\begin{matrix} 5 \\ -6 \\ -7 \end{matrix})$ ⋅ $(\begin{matrix} -4 \\ -1 \\ t \end{matrix})$ = -7⋅t -14 = 0 wird, also t= $- \frac{14}{7}$ = -2.

Der gesuchte Normalenvektor ist also $\vec{n}$ = $(\begin{matrix} -4 \\ -1 \\ -2 \end{matrix})$

Normalenvektor

Beispiel:

Finde einen Vektor, der sowohl zu $\vec{u}$ = $(\begin{matrix} 4 \\ 1 \\ 0 \end{matrix})$ als auch zu $\vec{v}$ = $(\begin{matrix} -3 \\ 3 \\ -5 \end{matrix})$ orthogonal ist (der Nullvektor ist nicht erlaubt).

Lösung einblenden

Weil beim Vektor $(\begin{matrix} 4 \\ 1 \\ 0 \end{matrix})$ in der x₃-Koordinate eine 0 steht, wäre ja der Vektor $(\begin{matrix} -1 \\ 4 \\ t \end{matrix})$ für jedes t orthogonal zu $(\begin{matrix} 4 \\ 1 \\ 0 \end{matrix})$ , denn $(\begin{matrix} 4 \\ 1 \\ 0 \end{matrix})$ ∘ $(\begin{matrix} -1 \\ 4 \\ t \end{matrix})$ = $4 \cdot (-1) + 1 \cdot 4 + 0 \cdot t = -4 +4 +0 = 0$ .

Nun müssen wir noch das t so bestimmen, dass auch das Skalarprodukt mit dem Vektor $(\begin{matrix} -3 \\ 3 \\ -5 \end{matrix})$ ⋅ $(\begin{matrix} -1 \\ 4 \\ t \end{matrix})$ = -5⋅t +15 = 0 wird, also t= $\frac{15}{5}$ = 3.

Der gesuchte Normalenvektor ist also $\vec{n}$ = $(\begin{matrix} -1 \\ 4 \\ 3 \end{matrix})$

Gerade in E, die senkrecht auf g ist

Beispiel:

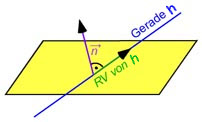Bestimme eine Gerade h, die in der Ebene E: $-4 x_{1} - 2 x_{2} - x_{3} = 14$ liegt und orthogonal zur Geraden g: $\vec{x} =$ $(\begin{matrix} -3 \\ -3 \\ 4 \end{matrix}) + t \cdot (\begin{matrix} 2 \\ 0 \\ 3 \end{matrix})$ verläuft.

Lösung einblenden

Da die gesuchte Gerade h in der Ebene E liegt und orthogonal zu g steht, muss der Richtungsvevtor $\vec{{rv}_{h}}$ der gesuchten Geraden h sowohl zum Normalenvektor $\vec{n}$ = $(\begin{matrix} -4 \\ -2 \\ -1 \end{matrix})$ von E als auch zum Richungsvektor $\vec{{rv}_{g}}$ = $(\begin{matrix} 2 \\ 0 \\ 3 \end{matrix})$ von g orthogonal stehen.

Weil beim Richungsvektor $\vec{{rv}_{g}}$ = $(\begin{matrix} 2 \\ 0 \\ 3 \end{matrix})$ in der x₂-Koordinaten eine 0 steht, wäre ja der Vektor $(\begin{matrix} 3 \\ t \\ -2 \end{matrix})$ für jedes t orthogonal zur Geraden, denn $(\begin{matrix} 2 \\ 0 \\ 3 \end{matrix})$ ∘ $(\begin{matrix} 3 \\ t \\ -2 \end{matrix})$ = $2 \cdot 3 + 0 \cdot t + 3 \cdot (-2) = 6 +0 -6 = 0$ .

Nun müssen wir noch das t so bestimmen, dass auch das Skalarprodukt mit dem Normalenvektor von E $(\begin{matrix} -4 \\ -2 \\ -1 \end{matrix})$ ⋅ $(\begin{matrix} 3 \\ t \\ -2 \end{matrix})$ = -2⋅t -10 = 0 wird, also t= $- \frac{10}{2}$ = $- 5$ . Der Richungsvektor der gesuchten Geraden h ist also $\vec{{rv}_{h}}$ = $(\begin{matrix} 3 \\ -5 \\ -2 \end{matrix})$ .

Da $\vec{n}$ ⋅ $\vec{{rv}_{h}}$ = $(\begin{matrix} 2 \\ 0 \\ 3 \end{matrix})$ ∘ $(\begin{matrix} 3 \\ -5 \\ -2 \end{matrix})$ = $2 \cdot 3 + 0 \cdot (-5) + 3 \cdot (-2) = 6 +0 -6 = 0$ ist, liegt also unsere gesuchte Gerade h entweder parallel zu Ebene E oder sie liegt in ihr. Wir brauchen also noch einen Aufpunkt, der in E liegt, so dass auch die ganze Gerade in E liegen muss.

Wir können jetzt also einen beliebigen Punkt der Ebene E als Aufpunkt für unsere gesuchte Gerade h nehmen:
$(-3 | -3 | 4)$ liegt in E, da:

$-4 \cdot (-3) - 2 \cdot (-3) - 1 \cdot 4 = 14$

.

Die gesuchte Gerade ist also h: $\vec{x} =$ $(\begin{matrix} -3 \\ -3 \\ 4 \end{matrix}) + t \cdot (\begin{matrix} 3 \\ -5 \\ -2 \end{matrix})$

Ebene, die g beinhaltet und ortho zu F

Beispiel:

Bestimme eine Ebene E, in der die Gerade g: $\vec{x} =$ $(\begin{matrix} 4 \\ 2 \\ 3 \end{matrix}) + t \cdot (\begin{matrix} 6 \\ 0 \\ 4 \end{matrix})$ liegt und die orthogonal zur Ebene F: $-2 x_{1} - 4 x_{2} + 4 x_{3} = -3$ steht.

Lösung einblenden

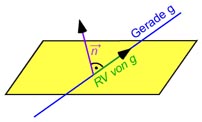Da die gesuchte Ebene die Gerade g beinhaltet und orthogonal zu F steht, muss der Normalenvektor $\vec{n}$ der gesuchten Ebene E sowohl zum Normalenvektor $\vec{n_{F}}$ = $(\begin{matrix} -2 \\ -4 \\ 4 \end{matrix})$ von F als auch zum Richungsvektor $\vec{rv}$ = $(\begin{matrix} 6 \\ 0 \\ 4 \end{matrix})$ von g orthogonal stehen.

Weil beim Richungsvektor $\vec{rv}$ = $(\begin{matrix} 6 \\ 0 \\ 4 \end{matrix})$ in der x₂-Koordinaten eine 0 steht, wäre ja der Vektor $(\begin{matrix} 4 \\ t \\ -6 \end{matrix})$ für jedes t orthogonal zur Geraden, denn $(\begin{matrix} 6 \\ 0 \\ 4 \end{matrix})$ ∘ $(\begin{matrix} 4 \\ t \\ -6 \end{matrix})$ = $6 \cdot 4 + 0 \cdot t + 4 \cdot (-6) = 24 +0 -24 = 0$ .

Nun müssen wir noch das t so bestimmen, dass auch das Skalarprodukt mit dem Normalenvektor von F $(\begin{matrix} -2 \\ -4 \\ 4 \end{matrix})$ ⋅ $(\begin{matrix} 4 \\ t \\ -6 \end{matrix})$ = -4⋅t -32 = 0 wird, also t= $- \frac{32}{4}$ = $- 8$ . Der Normalenvektor der gesuchten Ebene ist also $\vec{n_{E}}$ = $(\begin{matrix} 4 \\ -8 \\ -6 \end{matrix})$ , die Ebenengleichung also: $4 x_{1} - 8 x_{2} - 6 x_{3} = d$ .

Da $\vec{rv}$ ⋅ $\vec{n_{E}}$ = $(\begin{matrix} 6 \\ 0 \\ 4 \end{matrix})$ ∘ $(\begin{matrix} 4 \\ -8 \\ -6 \end{matrix})$ = $6 \cdot 4 + 0 \cdot (-8) + 4 \cdot (-6) = 24 +0 -24 = 0$ ist, liegt also g entweder parallel zu unserer gesuchten Ebene E oder sie liegt in ihr. Wenn der Aufpunkt $(4 | 2 | 3)$ in E liegt, muss also auch die ganze Gerade in E liegen. Wir setzen also $(4 | 2 | 3)$ in E ein:

$4 \cdot 4 - 8 \cdot 2 - 6 \cdot 3 = d$

und erhalten d=-18.

Die gesuchte Ebene ist also E: $4 x_{1} - 8 x_{2} - 6 x_{3} = -18$

Gerade mit gl. Abstand zu E und F

Beispiel:

Der Punkt P $(-7 | -8 | 4)$ hat sowohl von der Ebene E: $-4 x_{1} - 4 x_{2} + 2 x_{3} = -4$ als auch von der Ebene F: $2 x_{1} - 4 x_{2} - 4 x_{3} = -70$ den gleichen Abstand d = 12. Bestimme die Gleichung einer Geraden, deren Punkte auch alle den Abstand d=12 von E und von F haben.

Lösung einblenden

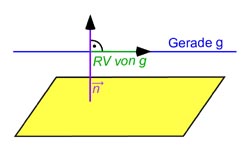
Wenn die Punkte der gesuchten Geraden alle den gleichen Abstand zu E haben, dann muss die Gerade parallel zu E sein. Der Richtungsvektor $\vec{u}$ muss also orthogonal zum Normalenvektor von E sein: $\vec{u}$ ⋅ $(\begin{matrix} -4 \\ -4 \\ 2 \end{matrix})$ = 0.

Das gleiche gilt natürlich auch für die Ebene F, auch zu dieser Ebene muss g parallel sein. Auch hier muss also gelten, dass der Richtungsvektor $\vec{u}$ orthogonal zum Normalenvektor von F sein muss:
$\vec{u}$ ⋅ $(\begin{matrix} 2 \\ -4 \\ -4 \end{matrix})$ = 0.

Wir suchen also einen Richtungsvektor, der sowohl orthogonal zu $(\begin{matrix} -4 \\ -4 \\ 2 \end{matrix})$ als auch zu $(\begin{matrix} 2 \\ -4 \\ -4 \end{matrix})$ ist. Dieses Problem kennen wir ja bereits und können wir mit dem Vektorprodukt (Kreuzprodukt) lösen:

$\vec{u} = (\begin{matrix} -4 \\ -4 \\ 2 \end{matrix}) \times (\begin{matrix} 2 \\ -4 \\ -4 \end{matrix}) = (\begin{matrix} - 4 \cdot (- 4) - 2 \cdot (- 4) \\ 2 \cdot 2 - (- 4) \cdot (- 4) \\ - 4 \cdot (- 4) - (- 4) \cdot 2 \end{matrix}) = (\begin{matrix} 16 + 8 \\ 4 - 16 \\ 16 + 8 \end{matrix}) = (\begin{matrix} 24 \\ - 12 \\ 24 \end{matrix})$ = -12⋅ $(\begin{matrix} -2 \\ 1 \\ -2 \end{matrix})$

Als Stützvektor dieser Geraden brauchen wir einen Punkt, der von beiden Ebenen den gleichen Abstand d=12 hat. Dafür können wir natürlich einfach den Ortsvektor des gegebenen Punkts $\vec{OP}$ = $(\begin{matrix} -7 \\ -8 \\ 4 \end{matrix})$ nehmen.

Eine mögliche Gleichung solch einer Gerade wäre also g: $\vec{x} =$ $(\begin{matrix} -7 \\ -8 \\ 4 \end{matrix}) + t \cdot (\begin{matrix} -2 \\ 1 \\ -2 \end{matrix})$ .

Ebene, die g beinhaltet und ortho zu F

Beispiel:

Bestimme eine Ebene E, in der die Gerade g: $\vec{x} =$ $(\begin{matrix} 0 \\ -2 \\ -4 \end{matrix}) + t \cdot (\begin{matrix} 0 \\ 2 \\ 1 \end{matrix})$ liegt und die orthogonal zur Ebene F: $4 x_{1} + 4 x_{2} - 6 x_{3} = 3$ steht.

Lösung einblenden

Da die gesuchte Ebene die Gerade g beinhaltet und orthogonal zu F steht, muss der Normalenvektor $\vec{n}$ der gesuchten Ebene E sowohl zum Normalenvektor $\vec{n_{F}}$ = $(\begin{matrix} 4 \\ 4 \\ -6 \end{matrix})$ von F als auch zum Richungsvektor $\vec{rv}$ = $(\begin{matrix} 0 \\ 2 \\ 1 \end{matrix})$ von g orthogonal stehen.

Weil beim Richungsvektor $\vec{rv}$ = $(\begin{matrix} 0 \\ 2 \\ 1 \end{matrix})$ in der x₁-Koordinaten eine 0 steht, wäre ja der Vektor $(\begin{matrix} t \\ -1 \\ 2 \end{matrix})$ für jedes t orthogonal zur Geraden, denn $(\begin{matrix} 0 \\ 2 \\ 1 \end{matrix})$ ∘ $(\begin{matrix} t \\ -1 \\ 2 \end{matrix})$ = $0 \cdot t + 2 \cdot (-1) + 1 \cdot 2 = 0 -2 +2 = 0$ .

Nun müssen wir noch das t so bestimmen, dass auch das Skalarprodukt mit dem Normalenvektor von F $(\begin{matrix} 4 \\ 4 \\ -6 \end{matrix})$ ⋅ $(\begin{matrix} t \\ -1 \\ 2 \end{matrix})$ = 4⋅t -16 = 0 wird, also t= $\frac{16}{4}$ = $4$ . Der Normalenvektor der gesuchten Ebene ist also $\vec{n_{E}}$ = $(\begin{matrix} 4 \\ -1 \\ 2 \end{matrix})$ , die Ebenengleichung also: $4 x_{1} - x_{2} + 2 x_{3} = d$ .

Da $\vec{rv}$ ⋅ $\vec{n_{E}}$ = $(\begin{matrix} 0 \\ 2 \\ 1 \end{matrix})$ ∘ $(\begin{matrix} 4 \\ -1 \\ 2 \end{matrix})$ = $0 \cdot 4 + 2 \cdot (-1) + 1 \cdot 2 = 0 -2 +2 = 0$ ist, liegt also g entweder parallel zu unserer gesuchten Ebene E oder sie liegt in ihr. Wenn der Aufpunkt $(0 | -2 | -4)$ in E liegt, muss also auch die ganze Gerade in E liegen. Wir setzen also $(0 | -2 | -4)$ in E ein:

$4 \cdot 0 - 1 \cdot (-2) + 2 \cdot (-4) = d$

und erhalten d=-6.

Die gesuchte Ebene ist also E: $4 x_{1} - x_{2} + 2 x_{3} = -6$

Achsenpunkt für parallele Gerade

Beispiel:

Gegeben sind die Ebene E: $- 2 x_{2} + 4 x_{3} = 4$ und der Punkt P $(2 | 6 | -1)$ . P liegt nicht in E.

Bestimme eine Gerade g, die parallel zu E liegt, den Punkt P enthält und die x₂-Achse schneidet.

Lösung einblenden

Wir nennen den Schnittpunkt der gesuchten Gerade mit der x₂-Achse Q_c(0|c|0). Damit muss $\vec{Q_{c} P}$ = $(\begin{matrix} 2 \\ 6 - c \\ -1 \end{matrix})$ der Richtungsvektor der gesuchten Gerade sein.

Wenn diese Gerade nun parallel zur Ebene E sein soll, muss der Normalenvektor von E orthogonal zu $\vec{Q_{c} P}$ sein, also gilt:

0 = $(\begin{matrix} 0 \\ -2 \\ 4 \end{matrix})$ ⋅ $(\begin{matrix} 2 \\ 6 - c \\ -1 \end{matrix})$ = $0 \cdot 2 - 2 \cdot (6 - c) + 4 \cdot (- 1)$ = $0 - 2 (6 - c) - 4$

$0 - 2 (6 - c) - 4$	=	0
$- 12 + 2 c - 4$	=	0
$2 c - 16$	=	0	\| $+ 16$
$2 c$	=	$16$	\|: $2$
$c$	=	$8$

Damit ist der Richtungsvektor der gesuchten Gerade $\vec{Q_{8} P}$ = $(\begin{matrix} 2 \\ 6 -8 \\ -1 \end{matrix})$ = $(\begin{matrix} 2 \\ -2 \\ -1 \end{matrix})$

Die gesuchte Gerade ist also h: $\vec{x} =$ $(\begin{matrix} 2 \\ 6 \\ -1 \end{matrix}) + t \cdot (\begin{matrix} 2 \\ -2 \\ -1 \end{matrix})$

Rechteck in einer Ebene finden

Beispiel:

Das Rechteck ABCD mit A $(0 | 0 | 0)$ und B $(0 | 3 | -4)$ liegt in der Ebene E: $x_{1} = 0$ und hat den Flächeninhalt 50.
Bestimme die Koordinaten eines möglichen Punkts C.

Lösung einblenden

Der Vektor $\vec{BC}$ muss orthogonal zu $\vec{AB}$ = $(\begin{matrix} 0 \\ 3 \\ -4 \end{matrix})$ sein, weil ABCD ja ein Rechteck mit lauter rechten Winkeln ist. Außerdem muss $\vec{BC}$ aber auch noch orthogonal zum Normalenvektor der Ebene $\vec{n}$ = $(\begin{matrix} 1 \\ 0 \\ 0 \end{matrix})$ sein, weil ja alle Punkte und deren Verbindungsvektoren in der Ebene liegen.

Und die Richtung, die sowohl orthogonal zu $(\begin{matrix} 0 \\ 3 \\ -4 \end{matrix})$ als auch zu $(\begin{matrix} 1 \\ 0 \\ 0 \end{matrix})$ sein muss, können wir mit dem Vektorprodukt berechnen:

k⋅ $\vec{BC} = (\begin{matrix} 0 \\ 3 \\ -4 \end{matrix}) \times (\begin{matrix} 1 \\ 0 \\ 0 \end{matrix}) = (\begin{matrix} 3 \cdot 0 - (- 4) \cdot 0 \\ - 4 \cdot 1 - 0 \cdot 0 \\ 0 \cdot 0 - 3 \cdot 1 \end{matrix}) = (\begin{matrix} 0 + 0 \\ - 4 + 0 \\ 0 - 3 \end{matrix}) = (\begin{matrix} 0 \\ - 4 \\ - 3 \end{matrix})$

Die Länge des Vektors können wir über den Flächeninhalt berechnen:

A = $| (\begin{matrix} 0 \\ 3 \\ -4 \end{matrix}) |$ ⋅ $| k \cdot (\begin{matrix} 0 \\ 4 \\ 3 \end{matrix}) |$ = 50

mit $| (\begin{matrix} 0 \\ 3 \\ -4 \end{matrix}) |$ = $\sqrt{0^{2} + 3^{2} + {(-4)}^{2}} = \sqrt{25} = 5$ und $| (\begin{matrix} 0 \\ 4 \\ 3 \end{matrix}) |$ = $\sqrt{0^{2} + 4^{2} + 3^{2}} = \sqrt{25} = 5$ gilt somit:

5 ⋅ k⋅5 = 50 | :25

k = $\frac{50}{25}$ = 2

Für den Ortsvektor des gesuchten Punkts C gilt somit:
$\vec{0C}$ = $\vec{0B}$ + 2⋅ $(\begin{matrix} 0 \\ 4 \\ 3 \end{matrix})$ = $(\begin{matrix} 0 \\ 3 \\ -4 \end{matrix})$ + $(\begin{matrix} 0 \\ 8 \\ 6 \end{matrix})$ = $(\begin{matrix} 0 \\ 11 \\ 2 \end{matrix})$
bzw. $\vec{0C'}$ = $\vec{0B}$ - 2⋅ $(\begin{matrix} 0 \\ 4 \\ 3 \end{matrix})$ = $(\begin{matrix} 0 \\ 3 \\ -4 \end{matrix})$ + $(\begin{matrix} 0 \\ -8 \\ -6 \end{matrix})$ = $(\begin{matrix} 0 \\ -5 \\ -10 \end{matrix})$

Die Koordinaten von C sind somit C $(0 | 11 | 2)$ oder C' $(0 | -5 | -10)$ .

Aufgabenbeispiele von Zwei Bedingungen

Normalenvektor ohne Kreuzprodukt

Normalenvektor

Gerade in E, die senkrecht auf g ist

Ebene, die g beinhaltet und ortho zu F

Gerade mit gl. Abstand zu E und F

Ebene, die g beinhaltet und ortho zu F

Achsenpunkt für parallele Gerade

Rechteck in einer Ebene finden