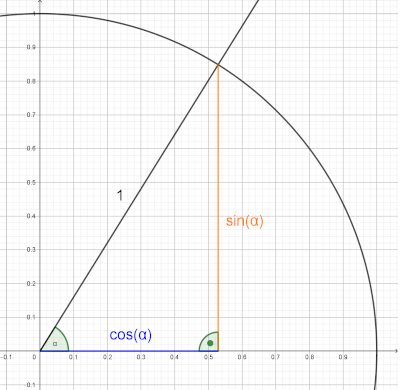
Nach dem Satz des Pythagoras im Einheitskreis gilt immer:

(sin(α))² + (cos(α))² = 1

Umgestellt nach sin(α):

(sin(α))² = 1 - (cos(α))²

= 1 - ${\left(\frac{\sqrt{91}}{10}\right)}^2$

= 1 - $\frac{91}{100}$

= $\frac{9}{100}$

Damit glit für sin(α):

sin(α) = $\frac{3}{10}$ = 0.3

Am Einheitskreis kann man die Werte für sin(28°) und cos(28°) ablesen:

cos(28°) ist der x-Wert des Schnittpunktes der roten Geraden mit dem (blauen) Einheitskreis, also die Länge der orangen Strecke.
Am besten ablesen kann man diesen Wert, wenn man die (grüne) senkrechte Linie zur x-Aches verfolgt:

cos(28°) ≈ 0.88

Am Einheitskreis kann man den Wert für α ablesen:

cos(α) = 0.3 bedeutet, dass der x-Wert des Schnittpunktes der roten Geraden mit dem (blauen) Einheitskreis, 0.3 sein muss. Wenn man den den Winkel auf 72.5° setzt, so sieht man, dass der cos(72.5)°, also die Länge der orangen Strecke eben ≈ 0.3 ist.

cos(72.5°) ≈ 0.3

Am Einheitskreis kann man die Werte für sin(62°) und cos(62°) ablesen:

sin(62°) ist der y-Wert des Schnittpunktes der roten Geraden mit dem (blauen) Einheitskreis, also die (vorzeichenbehaftete) Länge der grünen Strecke.
Am besten ablesen kann man diesen Wert, wenn man die (orange) waagrechte Linie zur y-Aches verfolgt:

sin(62°) ≈ 0.88

Am Einheitskreis kann man die beiden Werte für α ablesen:

sin(α) = 0.55 bedeutet, dass der y-Wert des Schnittpunktes der roten Geraden mit dem (blauen) Einheitskreis 0.55 sein muss. In der Skizze sieht man, dass dies sowohl für α₁ = 33.4° als auch für α₂ = 146.6° der Fall ist, weil in beiden Fällen die Länge der grünen Strecke eben ≈ 0.55 ist.

sin(33.4°) ≈ 0.55 und sin(146.6°) ≈ 0.55

Da ja ein (Einheits-)Kreis 360° als Gesamtwinkel hat, gelangt man nach weiterer Drehung um +360° oder -360° wieder genau zum ursprünglichen Punkt auf dem Einheitskreis (der somit natürlich wieder die gleichen Sinus- und Kosinuswerte besitzt).

Und da unser Ausgangswinkel -520° < 0° ist, müssen wir eben so lange 360° addieren, bis unser Winkel zwischen 0 und 360° ist:

α = -520 + 360° + 360° = 200°

Man erkennt am Schaubild rechts, dass die beiden Winkel mit dem gleichen Sinuswert (grüner senkrechter Strich) symmetrisch zur y-Achse liegen.

Wenn man also den (braunen) Ausgangswinkel 130° an der y-Achse spiegelt, erhält man wieder 130°, allerdings diesemal zwischen der negativen x-Achse und dem pinken Strich. Den gesuchten Winkel misst man ja aber immer zwischen der positiven x-Achse und dem Strich, und das ist dann ja gerade das was noch zu den 180° fehlt:

Wir können also immer einfach 180°- den gegebenen Winkel rechnen, um auf den Winkel mit dem gleichen Sinuswert zu kommen: hier also

α = 180° - 130° = 50°

So erhalten wir die Funktion f(α) = 200 ⋅ sin(α).

1. Gesuchte Höhe zur Zeit t = 17 ms

Um nun die gesuchte Höhe zur gegebenen Zeit zu berechnen, müssen wir zuerst den Winkel bestimmen, der nach 17 ms erreicht wurde. Weil ja immer gleich viel Winkel pro Zeit 'zurückgelegt' wird, genügt hierfür ein Dreisatz :

20 ms ≙ 360°
1 ms ≙ $\frac{\mathrm{360}}{\mathrm{20}}$ ° = 18°
17 ms ≙ 18 ⋅ 17° ≈ 306°

sin(306°) ≈ -0.81, entsprechend ist 200 ⋅ sin(306°) ≈ -161.8

Also ist nach 17 ms der y-Wert -161,8 V.

2. Gesuchte Zeit zur gegebenen Höhe h = 180 V

Wir können nun nach dem Winkel suchen, bei dem f(α) = 200 ⋅ sin(α) = 180 gilt.

200 ⋅ sin(α) = 180 |: 200

sin(α) = 0.9 | arcsin(⋅) (WTR: sin^-1)

α ≈ 64.2°

Jetzt müssen wir den Dreisatz eben anders rum wie oben machen:

360° ≙ 20 ms
1 ° ≙ $\frac{\mathrm{20}}{\mathrm{360}}$ ms = $\frac{1}{18}$ ms
64.2° ≙ $\frac{1}{18}$ ⋅ 64.2 ms ≈ 3.567 ms

Somit ist nach 3,567 ms die Höhe h = 180 V erreicht.

Am Schaubild sehen wir, dass es aber auch noch einen zweiten Winkel β mit 200 ⋅ sin(α) = 180 bzw. sin(β) = 0.9. Durch die Symmetrie erkennen wir, dass dieser weitere Winkel β gleich weit von 180° entfernt ist wie α, es gilt also β = 180°-α = 180°-64.2 = 115.8°.

Auch hier müssen wir wieder mit dem Dreisatz die zugehörige Zeit ermitteln:

360° ≙ 20 ms
1 ° ≙ $\frac{\mathrm{20}}{\mathrm{360}}$ ms = $\frac{1}{18}$ ms
115.8° ≙ $\frac{1}{18}$ ⋅ 115.8 ms ≈ 6.433 ms

Somit ist nach auch 6,433 ms die Höhe h = 180 V erreicht.