Aufgabenbeispiele von 2. Strahlensatz
Durch Aktualisieren des Browsers (z.B. mit Taste F5) kann man neue Beispielaufgaben sehen
2. Strahlensatz (gleiche Seite)
Beispiel:
Die beiden blauen Geraden sind parallel.
Berechne x.
Nach dem 2. Strahlensatz gilt:
=
| = | |||
| = | |⋅ 15.6 | ||
| = |
2. Strahlensatz (2 Seiten)
Beispiel:
Die beiden blauen Geraden sind parallel.
Berechne x.
Nach dem 2. Strahlensatz gilt:
=
| = | |||
| = | |⋅ 10 | ||
| = | = 8 |
2. Strahlensatz (gleiche Seite)
Beispiel:
Die beiden blauen Geraden sind parallel.
Berechne x.
Nach dem 2. Strahlensatz gilt:
=
D=R\{
| = | |||
| = |
Wir multiplizieren den Nenner weg!
| = | |⋅( ) | ||
| = | |||
| = |
| = | | | ||
| = | |:() | ||
| = |
(Alle Lösungen sind auch in der Definitionsmenge).
doppelter Strahlensatz (klein)
Beispiel:
Die beiden blauen Geraden sind parallel.
Berechne x und y.
Nach dem 1. Strahlensatz gilt:
=
D=R\{
| = | |||
| = |
Wir multiplizieren den Nenner weg!
| = | |⋅( ) | ||
| = | |||
| = |
| = | | | ||
| = | |:() | ||
| = |
(Alle Lösungen sind auch in der Definitionsmenge).
Nach dem 2. Strahlensatz gilt:
=
| = | |||
| = | |⋅ 33 | ||
| = |
Strahlensatz Anwendungen
Beispiel:
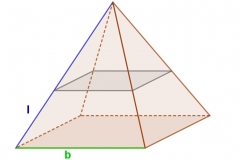
Die Grundfläche einer senkrechten quadratischen Pyramide ist b=31,5 m lang. Parallel zur Grundfläche wird eine zweite Ebene eingezogen, deren Grundfläche ein Quadrat mit Seitenlänge 18 m ist. Die Kantenlänge des oberen pyramidenformigen Stocks beträgt 8 m. Bestimme die Kantenlänge des unteren Stockwerks (in Form eines Pyramidenstumpfs).
Wenn man in die Skizze ein paar Strecken einzeichnet, erkennt man eine Strahlensatzfigur:
Dabei gilt nach dem 2. Strahlensatz:
= bzw. =
Aus dem Text können wir herauslesen:
l2 = 8
b2 = 18
b = 31.5
Gesucht ist die Kantenlänge des unteren Stocks der Pyramide. Wir wählen also l1 als x.
Jetzt können wir die Werte in die obige Strahlensatzgleichung einsetzen und erhalten:
=
| = | |||
| = | |||
| = | |⋅ 8 | ||
| = | |||
| = | | | ||
| = |
l1 ist also .
Die Lösung ist somit: 6
