Aufgabenbeispiele von umwandeln in Scheitelform
Durch Aktualisieren des Browsers (z.B. mit Taste F5) kann man neue Beispielaufgaben sehen
Nullstellen mit Nullprodukt
Beispiel:
Bestimme die Nullstellen der quadratischen Funktion f mit
Hier kann man x ausklammern und den Satz vom Nullprodukt anwenden
| = | |||
| = |
Ein Produkt ist genau dann =0, wenn mindestens einer der beiden Faktoren =0 ist.
1. Fall:
| x1 | = |
2. Fall:
| = | | | ||
| x2 | = |
L={
;
Nullstellen und Scheitel (Nullprodukt)
Beispiel:
Bestimme die Nullstellen und dann den Scheitel der quadratischen Funktion f mit
Hier kann man x ausklammern und den Satz vom Nullprodukt anwenden
| = | |||
| = |
Ein Produkt ist genau dann =0, wenn mindestens einer der beiden Faktoren =0 ist.
1. Fall:
| x1 | = |
2. Fall:
| = | | | ||
| x2 | = |
L={
;
Wegen der Symmetrie von Parabeln wissen wir, dass der Scheitel genau in der Mitte zwischen den Nullstellen liegen muss. Wir berechen also den Mittelwert der beiden Nullstellen = -1.5 und erhalten so den x-Wert des Scheitels.
Der Scheitel hat also die Koordinaten S(-1.5|f(-1.5)) mit f(-1.5) = = = -2.25.
Als Ergebnisse erhalten wir also: Nullstellen: x1=-3 und x2=0 , Scheitel: S(-1.5|-2.25).
x²+bx+c -> Scheitelform
Beispiel:
Bestimme die Koordinaten des Scheitels der Parabel von der Funktion f mit .
1. Weg
Man erweitert die ersten beiden Summanden ( ) zu einem 'binomischen Formel'-Term. Dazu teilt man die durch 2x und quadriert diese Ergebnis 1 zu 1. Diese 1 fügt man dann an dritter Stelle in die Summe ein. So erhält man einen Term der Form x² ± 2xb + b², den man mit der binomischen Formel als (x ± b)² schreiben kann. Damit der Funktionsterm aber nicht verändert wird muss man die 1, die man an 3. Stelle eingefügt hat, danach auch wieder abziehen.
=
=
=
Jetzt kann man den Scheitel leicht ablesen: S(-1|2).
2. Weg
Wir betrachten nun nur . Deren Parabel sieht ja genau gleich aus wie nur um nach oben/unten verschoben. Das heißt beide Parabeln haben ihren Scheitel an der gleichen x-Stelle.
Von können wir aber über Ausklammern und den Satz vom Nullprodukt sehr leicht die Nullstellen bestimmen.
| = | |||
| = |
Ein Produkt ist genau dann =0, wenn mindestens einer der beiden Faktoren =0 ist.
1. Fall:
| x1 | = |
2. Fall:
| = | | | ||
| x2 | = |
Aus Symmetriegründen muss der Scheitel genau in der Mitte zwischen den Nullstellen liegen, also S(-1|f(-1)).
f(-1) = = = 2
also: S(-1|2).
ax²+bx+c -> Scheitelform
Beispiel:
Bestimme die Koordinaten des Scheitels der Parabel von der Funktion f mit .
1. Weg
=
Man erweitert die ersten beiden Summanden ( ) zu einem 'binomischen Formel'-Term. Dazu teilt man die durch 2x und quadriert diese Ergebnis -1 zu 1. Diese 1 fügt man dann an dritter Stelle in die Summe ein. So erhält man einen Term der Form x² ± 2xb + b², den man mit der binomischen Formel als (x ± b)² schreiben kann. Damit der Funktionsterm aber nicht verändert wird muss man die 1, die man an 3. Stelle eingefügt hat, danach auch wieder abziehen.
=
=
=
=
Jetzt kann man den Scheitel leicht ablesen: S(1|1).
2. Weg
Wir betrachten nun nur . Deren Parabel sieht ja genau gleich aus wie nur um nach oben/unten verschoben. Das heißt beide Parabeln haben ihren Scheitel an der gleichen x-Stelle.
Von können wir aber über Ausklammern und den Satz vom Nullprodukt sehr leicht die Nullstellen bestimmen.
| = | |||
| = |
Ein Produkt ist genau dann =0, wenn mindestens einer der beiden Faktoren =0 ist.
1. Fall:
| x1 | = |
2. Fall:
| = | | | ||
| x2 | = |
Aus Symmetriegründen muss der Scheitel genau in der Mitte zwischen den Nullstellen liegen, also S(1|f(1)).
f(1) = = = 1
also: S(1|1).
Extremwertaufgaben (Anwend.)
Beispiel:
Ein Rechteck hat den Umfang cm. Wie breit muss es sein, damit der Flächeninhalt des Rechtecks am größten wird.
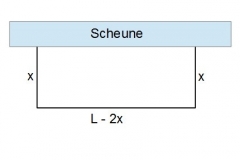
1. Weg
=
Man erweitert die ersten beiden Summanden ( ) zu einem 'binomischen Formel'-Term. Dazu teilt man die durch 2x und quadriert diese Ergebnis -75 zu 5625. Diese 5625 fügt man dann an dritter Stelle in die Summe ein. So erhält man einen Term der Form x² ± 2xb + b², den man mit der binomischen Formel als (x ± b)² schreiben kann. Damit der Funktionsterm aber nicht verändert wird muss man die 5625, die man an 3. Stelle eingefügt hat, danach auch wieder abziehen.
=
=
=
=
Jetzt kann man den Scheitel leicht ablesen: S(75|5625).
2. Weg
Von können wir aber über Ausklammern und den Satz vom Nullprodukt sehr leicht die Nullstellen bestimmen.
| = | |||
| = |
Ein Produkt ist genau dann =0, wenn mindestens einer der beiden Faktoren =0 ist.
1. Fall:
| x1 | = |
2. Fall:
| = | | | ||
| = | |:() | ||
| x2 | = |
Aus Symmetriegründen muss der Scheitel genau in der Mitte zwischen den Nullstellen liegen, also S(75|f(75)).
f(75) = = = 5625
also: S(75|5625).
Für x=75 bekommen wir also mit 5625 einen extremalen Wert von
