Aufgabenbeispiele von Tangenten
Durch Aktualisieren des Browsers (z.B. mit Taste F5) kann man neue Beispielaufgaben sehen
Tangente anlegen (einfache Funktionen)
Beispiel:
Berechne die Tangentengleichung an den Graphen von f mit an der Stelle x= :
Zuerst braucht man die Ableitung von , also
=
Um die Steigung der Tangente zu erhalten, setzen wir den gegebenen x-Wert in die Ableitung ein:
=
Damit wissen wir nun schon, dass die Tangente die Gleichung t: y=
Um noch das c zu bestimmen, brauchen wir einen Punkt, den wir in die Gleichung einsetzen können.
Dazu müssen wir noch den y-Wert des Berührpunkts bestimmen, also
Wir erhalten so also den Punkt B(
Nun setzt man die errechnete Ableitung und die errechneten Punktkoordinaten in eine allgemeine Geradengleichung (y=mx+c) ein:
also c=
Damit erhält man als Geradengleichung für die Tangente: y=
Tangente anlegen (auch verkettete Fkt'n)
Beispiel:
Berechne die Tangentengleichung an den Graphen von f mit
Zuerst braucht man die Ableitung von
=
=
Um die Steigung der Tangente zu erhalten, setzen wir den gegebenen x-Wert in die Ableitung ein:
=
=
Damit wissen wir nun schon, dass die Tangente die Gleichung t: y=
Um noch das c zu bestimmen, brauchen wir einen Punkt, den wir in die Gleichung einsetzen können.
Dazu müssen wir noch den y-Wert des Berührpunkts bestimmen, also
Wir erhalten so also den Punkt B(
Nun setzt man die errechnete Ableitung und die errechneten Punktkoordinaten in eine allgemeine Geradengleichung (y=mx+c) ein:
also c=
Damit erhält man als Geradengleichung für die Tangente: y=
e-Funktionen: Tangente anlegen BF
Beispiel:
Berechne die Tangentengleichung an den Graphen von f mit
Zuerst braucht man die Ableitung von
=
=
=
=
Um die Steigung der Tangente zu erhalten, setzen wir den gegebenen x-Wert in die Ableitung ein:
=
=
=
Damit wissen wir nun schon, dass die Tangente die Gleichung t: y=
Um noch das c zu bestimmen, brauchen wir einen Punkt, den wir in die Gleichung einsetzen können.
Dazu müssen wir noch den y-Wert des Berührpunkts bestimmen, also
Wir erhalten so also den Punkt B(
Nun setzt man die errechnete Ableitung und die errechneten Punktkoordinaten in eine allgemeine Geradengleichung (y=mx+c) ein:
also c=
Damit erhält man als Geradengleichung für die Tangente: y=
e-Funktionen: Tangente anlegen
Beispiel:
Berechne die Tangentengleichung an den Graphen von f mit
Zuerst braucht man die Ableitung von
=
=
=
=
Um die Steigung der Tangente zu erhalten, setzen wir den gegebenen x-Wert in die Ableitung ein:
=
=
=
=
Damit wissen wir nun schon, dass die Tangente die Gleichung t: y=
Um noch das c zu bestimmen, brauchen wir einen Punkt, den wir in die Gleichung einsetzen können.
Dazu müssen wir noch den y-Wert des Berührpunkts bestimmen, also
Wir erhalten so also den Punkt B(
Nun setzt man die errechnete Ableitung und die errechneten Punktkoordinaten in eine allgemeine Geradengleichung (y=mx+c) ein:
also c=
Damit erhält man als Geradengleichung für die Tangente: y=
Normale anlegen
Beispiel:
Berechne die Gleichung der Normalen an den Graphen von f mit
Zuerst braucht man die Ableitung von
=
Um die Steigung der Tangente zu erhalten, setzen wir den gegebenen x-Wert in die Ableitung ein:
=
=
Um mit der Tangentensteigung die Steigung der darauf senkrecht stehenden Normalen zu berechnen, verwenden wir die Beziehung:
mn= -
also mn=
Damit wissen wir nun schon, dass die Normale die Gleichung t: y=
Um noch das c zu bestimmen, brauchen wir einen Punkt, den wir in die Gleichung einsetzen können.
Dazu müssen wir noch den y-Wert des Berührpunkts bestimmen, also
Wir erhalten so also den Punkt B(
Nun setzt man die errechnete Ableitung und die errechneten Punktkoordinaten in eine allgemeine Geradengleichung (y=mx+c) ein:
also c=
Damit erhält man als Geradengleichung für die Normale: y=
Tangente von außen anlegen
Beispiel:
Vom Punkt P(1|3) aus sollen Tangenten an den Graphen von f mit
Bestimme alle möglichen Berührpunkte und bestimme (exemplarisch) eine Tangentengleichung an einem dieser Berührpunkte.
Zuerst wird die Ableitung von f berechnet:
Wir kennen den Berührpunkt, in dem die gesuchte Tangente durch P(1|3) an das Schaubild von f angelegt wird, nicht. Deswegen nennen wir den x-Wert u. Der Funktionswert ist dann f(u), da der Berührpunkt ja auf dem Schaubild von f liegt. Außerdem muss die Ableitung in u ja gerade die Tangentensteigung sein, da B(u|f(u)) der Berührpunkt ist.
Wir können also P(1|3) als (x|y), den Berührpunkt B(u|f(u)) und m=f'(u)=
y=f´(u) ⋅(x-u)+f(u)
einsetzen:
3 =
Die Lösung der Gleichung:
eingesetzt in die Mitternachtsformel (a-b-c-Formel):
u1,2 =
u1,2 =
u1,2 =
u1 =
u2 =
L={
Man hat nun also die x-Werte der Berührpunkte. In diesen müssen nun noch Tangenten an den Graphen von f angelegt werden.
An der Stelle x=
- 1 :
Zuerst braucht man die Ableitung von
=
Um die Steigung der Tangente zu erhalten, setzen wir den gegebenen x-Wert in die Ableitung ein:
=
=
Damit wissen wir nun schon, dass die Tangente die Gleichung t: y=
Um noch das c zu bestimmen, brauchen wir einen Punkt, den wir in die Gleichung einsetzen können.
Dazu müssen wir noch den y-Wert des Berührpunkts bestimmen, also
Wir erhalten so also den Punkt B(
Nun setzt man die errechnete Ableitung und die errechneten Punktkoordinaten in eine allgemeine Geradengleichung (y=mx+c) ein:
also c=
Damit erhält man als Geradengleichung für die Tangente: y=
An der Stelle x=
3 :
Zuerst braucht man die Ableitung von
=
Um die Steigung der Tangente zu erhalten, setzen wir den gegebenen x-Wert in die Ableitung ein:
=
=
Damit wissen wir nun schon, dass die Tangente die Gleichung t: y=
Um noch das c zu bestimmen, brauchen wir einen Punkt, den wir in die Gleichung einsetzen können.
Dazu müssen wir noch den y-Wert des Berührpunkts bestimmen, also
Wir erhalten so also den Punkt B(
Nun setzt man die errechnete Ableitung und die errechneten Punktkoordinaten in eine allgemeine Geradengleichung (y=mx+c) ein:
also c=
Damit erhält man als Geradengleichung für die Tangente: y=
Tangente von außen Anwendungen
Beispiel:
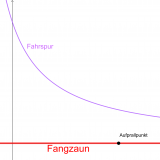
Ein Snowboarder fährt auf einer Linie, die im Modell durch den Graph der Funktion f mit f(x)=

Zuerst wird die Ableitung von f berechnet:
Wir kennen den Berührpunkt, in dem die gesuchte Tangente durch P(20|0) an das Schaubild von f angelegt wird, nicht. Deswegen nennen wir den x-Wert u. Der Funktionswert ist dann f(u), da der Berührpunkt ja auf dem Schaubild von f liegt. Außerdem muss die Ableitung in u ja gerade die Tangentensteigung sein, da B(u|f(u)) der Berührpunkt ist.
Wir können also P(20|0) als (x|y), den Berührpunkt B(u|f(u)) und m=f'(u)=
y=f´(u) ⋅(x-u)+f(u)
einsetzen:
0 =
Die Lösung der Gleichung:
|
|
= | |
|
|
|
|
= |
|
|: |
|
|
= |
|
L={
Es gibt also genau eine Berührstelle und somit ist x = 12.5 der x-Wert des Punktes im Modell, an dem der Snowboarder bestürtzt ist.
Normale von außen Anwendungen
Beispiel:
Bestimme den Punkt Q auf dem Graphen von f mit f(x) =
Der Punkt P liegt "außerhalb" der Parabel der Funktion f. Deswegen muss der Punkt P auf der Normalen an den Graph von f im gesuchten Kurvenpunkt Q liegen.
Gesucht ist der Kurvenpunkt auf dem Graph von f, dessen Normale durch den Punkt P(16
1
2
) verläuft.
Zuerst wird die Ableitung von f berechnet:
Wir kennen den Kurvenpunkt von Gf, an dem die gesuchte Normale durch P(
Da wir ja aber die Normale und nicht die Tangente suchen, müssen wir den negativen Kehrwert von f'(u) bilden, um die Steigung der Normalen zu erhalten.
mn = -
Wir können also P(
y = -
einsetzen:
Die Lösung der Gleichung:
|
|
= | ||
|
|
= | |
|
|
|
|
= | |: |
|
|
|
= | |
|
|
|
|
= |
|
=
|
L={
Man hat nun also die x-Werte der gesuchten Kurvenpunkte. Für die y-Werte muss man eben noch die x-Werte in die Originalfunktion f einsetzen:
f(
Wendetangente Anwendungen
Beispiel:
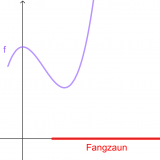
Ein Snowboarder fährt bei einem Rennen auf einer Linie, die im Modell durch den Graph der Funktion f mit f(x)=
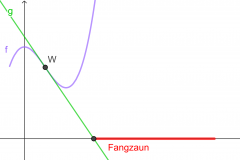
Wir suchen also nach dem Wendepunkt:
Als erstes leitet man die Funktion zwei mal ab.
=
Die notwendige Bedingung für einen Wendepunkt ist f''(x)=0.
(Wendestellen sind Extremstellen in der Ableitung, also haben Wendepunkten die Steigung 0 in f').
Man setzt nun also die zweite Ableitung gleich 0, um die einzig möglichen x-Werte für Wendepunkte zu bestimmen.
|
|
= | |
|
|
|
|
= |
|
|: |
|
|
= |
|
Die Lösung x=
Jetzt müssen wir noch die Tangente im Wendepunkt W(
Zuerst braucht man die Ableitung von
=
Um die Steigung der Tangente zu erhalten, setzen wir den gegebenen x-Wert in die Ableitung ein:
=
=
=
Damit wissen wir nun schon, dass die Tangente die Gleichung t: y=
Um noch das c zu bestimmen, brauchen wir einen Punkt, den wir in die Gleichung einsetzen können.
Dazu müssen wir noch den y-Wert des Berührpunkts bestimmen, also
Wir erhalten so also den Punkt B(
Nun setzt man die errechnete Ableitung und die errechneten Punktkoordinaten in eine allgemeine Geradengleichung (y=mx+c) ein:
also c=
Damit erhält man als Geradengleichung für die Tangente: y=
Jetzt müssen wir ja noch die Tangente mit der anderen Gerade y = 0 () schneiden, um den gesuchten x-Wert zu erhalten:
|
|
= | |
|
|
|
|
= |
|
|:( |
|
|
= |
|
Der gesuchte x-Wert () ist somit x ≈ 3.433.
Tangente von außen anlegen
Beispiel:
Vom Punkt P(-4|-17) aus sollen Tangenten an den Graphen von f mit
Bestimme alle möglichen Berührpunkte und bestimme (exemplarisch) eine Tangentengleichung an einem dieser Berührpunkte.
Zuerst wird die Ableitung von f berechnet:
Wir kennen den Berührpunkt, in dem die gesuchte Tangente durch P(-4|-17) an das Schaubild von f angelegt wird, nicht. Deswegen nennen wir den x-Wert u. Der Funktionswert ist dann f(u), da der Berührpunkt ja auf dem Schaubild von f liegt. Außerdem muss die Ableitung in u ja gerade die Tangentensteigung sein, da B(u|f(u)) der Berührpunkt ist.
Wir können also P(-4|-17) als (x|y), den Berührpunkt B(u|f(u)) und m=f'(u)=
y=f´(u) ⋅(x-u)+f(u)
einsetzen:
-17 =
Die Lösung der Gleichung:
eingesetzt in die Mitternachtsformel (a-b-c-Formel):
u1,2 =
u1,2 =
u1,2 =
u1 =
u2 =
L={
Man hat nun also die x-Werte der Berührpunkte. In diesen müssen nun noch Tangenten an den Graphen von f angelegt werden.
An der Stelle x=
- 6 :
Zuerst braucht man die Ableitung von
=
Um die Steigung der Tangente zu erhalten, setzen wir den gegebenen x-Wert in die Ableitung ein:
=
=
Damit wissen wir nun schon, dass die Tangente die Gleichung t: y=
Um noch das c zu bestimmen, brauchen wir einen Punkt, den wir in die Gleichung einsetzen können.
Dazu müssen wir noch den y-Wert des Berührpunkts bestimmen, also
Wir erhalten so also den Punkt B(
Nun setzt man die errechnete Ableitung und die errechneten Punktkoordinaten in eine allgemeine Geradengleichung (y=mx+c) ein:
also c=
Damit erhält man als Geradengleichung für die Tangente: y=
An der Stelle x=
- 2 :
Zuerst braucht man die Ableitung von
=
Um die Steigung der Tangente zu erhalten, setzen wir den gegebenen x-Wert in die Ableitung ein:
=
=
Damit wissen wir nun schon, dass die Tangente die Gleichung t: y=
Um noch das c zu bestimmen, brauchen wir einen Punkt, den wir in die Gleichung einsetzen können.
Dazu müssen wir noch den y-Wert des Berührpunkts bestimmen, also
Wir erhalten so also den Punkt B(
Nun setzt man die errechnete Ableitung und die errechneten Punktkoordinaten in eine allgemeine Geradengleichung (y=mx+c) ein:
also c=
Damit erhält man als Geradengleichung für die Tangente: y=

