Aufgabenbeispiele von Abstände
Durch Aktualisieren des Browsers (z.B. mit Taste F5) kann man neue Beispielaufgaben sehen
Abstand von A auf der Geraden AB
Beispiel:
Bestimme die Koordinaten der beiden Punkte, die auf der Geraden durch A und B liegen und von A den Abstand 9 haben.
Zuerst berechnen wir den Verbindungsvektor = und dessen Länge:
d=||=
Wir verkürzen nun den Vektor zu einem Einheitsvektor,
indem wir durch dessen Länge teilen:
==
Damit können wir die Gerade durch
A und B mit einem Einheitsvektor als Richtungsvektor darstellen:
.
Das heißt der Punkt X (vom Ortsvektor
) ist immer t Einheiten
vom Aufpunkt der Geraden A entfernt.
Für t=-9 und t=9 erhalten wir so also die gesuchten Punkte:
=+=. Der erste gesuchte Punkt ist also P1
Gerade mit best. Abstand zu E bestimmen
Beispiel:
Gegeben ist die Ebene E:
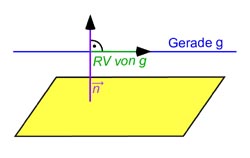
An der Skizze erkennt man, dass eine zu E parallele Gerade einen Richtungsvektor haben muss, der orthogonal zum Normalenvektor
Davon gibt es natürlich ziemlich viele, einer davon ist z.B.
denn
Jetzt brauchen wir als Stützvektor noch einen Punkt, der den Abstand d=7 von der Ebene E hat.
Dazu suchen wir zuerst mal einen beliebigen Punkt der Ebene, z.B. einen Spurpunkt PE
Die Länge des Normalenvektors berechnen wir mit |
Wenn wir also von PE
Eine mögliche Gerade wäre also g:
Abstand Punkt - Ebene E (mit Hesse-Form)
Beispiel:
Bestimme den Abstand des Punktes
P
Wir berechnen den Abstand zwischen Punkt und Ebene mittels der Hesse'schen Normalenform.
Abstand Punkt - Ebene E (mit Lotfußpunkt)
Beispiel:
Bestimme den Abstand des Punktes P
Berechne dabei auch den Lotfußpunkt.
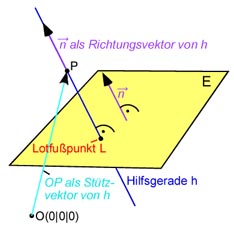 Der Normalenvektor der Ebene ist:
Der Normalenvektor der Ebene ist:
Wir bilden eine Gerade mit diesem Normalenvektor als Richtungsvektor, welche durch unseren Punkt
Nun berechnen wir den Durchstoßpunkt dieser Geraden mit unserer Ebene E:
Gesucht ist der Durchstoßpunkt zwischen der Geraden g:
Wir setzen einen allgemeinen Geradenpunkt der Geraden
|
|
= |
|
|
|
|
= |
|
|
|
|
= |
|
|
|
|
|
= | |: |
|
|
|
= |
Den Durchstoßpunkt erhalten wir, indem wir dieses t in die Geradengleichung bzw. in den allg. Geradenpunkt
=> D
Dieser Durchstoßpunkt D ist der gesuchte Lotfußpunkt L
Nun ist nur noch der Abstand zwischen diesem Lotfußpunkt L und unserem Punkt P
d=|
Abstand Pkt-Ebene + 2. Pkt mit d
Beispiel:
Bestimme den Abstand des Punktes P
Gib einen weiteren Punkt Q an, der den gleichen Abstand zu E hat.
 Der Normalenvektor der Ebene ist:
Der Normalenvektor der Ebene ist:
Wir bilden eine Gerade mit diesem Normalenvektor als Richtungsvektor, welche durch unseren Punkt
Nun berechnen wir den Durchstoßpunkt dieser Geraden mit unserer Ebene E:
Gesucht ist der Durchstoßpunkt zwischen der Geraden g:
Wir setzen einen allgemeinen Geradenpunkt der Geraden
|
|
= |
|
|
|
|
= |
|
|
|
|
= |
|
|
|
|
|
= |
|
|: |
|
|
= |
|
Den Durchstoßpunkt erhalten wir, indem wir dieses t in die Geradengleichung bzw. in den allg. Geradenpunkt
=> D
Dieser Durchstoßpunkt D ist der gesuchte Lotfußpunkt L
Nun ist nur noch der Abstand zwischen diesem Lotfußpunkt L und unserem Punkt P
d=|
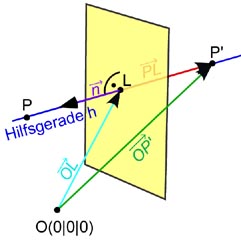 Wenn wir nun diesen Vektor
Wenn wir nun diesen Vektor
Der Punkt Q
Pyramidenvolumen rückwärts
Beispiel:
Eine gerade (senkrechte) Pyramide hat die quadratische Grundfläche ABCD mit A
Ihr Volumen beträgt 36 VE.
Bestimme die Koordinaten von einer der beiden möglichen Spitzen der Pyramide.
Man erkennt, dass alle 4 Punkte den x3-Wert 0 haben. Die quadratische Grundfläche liegt also in der Ebene: x3 = 0.
Eine gerade (senkrechte) Pyramide bedeutet, dass der Mittelpunkt der Punkt der Grundfläche mit den kleinsten Abstand zur Spitze S der Pyramide ist (S liegt direkt "über dem"/orthogonal zum Mittelpunkt)
Als Mittelpunkt können wir beim Quadrat die Mitte zwischen A und C oder B und D wählen: .
Da
Um die Höhe der Pyramide zu berechnen, setzen wir einfach alle bekannten Größen in die Volumenformel der Pyramide ein:
V =
36 =
36 =
3 = h
Weil der Normalenvektor
Die gesuchte Spitze der Pyramide ist also bei S
Theoretisch kann man die Spitze auch nach unten machen, dann müsste man eben 3 mal den Gegenvektor von
Kegelvolumen rückwärts
Beispiel:
Die kreisförmige Grundfläche eines geraden (senkrechten) Kegels liegt in der Ebene E:
M
Bestimme die Koordinaten von einer der beiden möglichen Spitzen des Kegels.
Ein gerader (senkrechter) Kegel bedeutet, dass der Mittelpunkt M
Da
Um die Höhe der Pyramide zu berechnen, setzen wir einfach alle bekannten Größen in die Volumenformel des Kegels ein:
V =
4123.34 =
4123.34 =
17.5 ≈ h
Die Länge des Normalenvektors
Man muss also 2.5 mal den Normalenvektor zum Ortsvektor des Grundflächenmittelpunkts M addieren, um auf den Ortsvektor der Pyramidenspitze S zu kommen.
Die gesuchte Spitze der Pyramide ist also bei S
Theoretisch kann man die Spitze auch nach unten machen, dann müsste man eben 2.5 mal den Gegenvektor von
Abstand Punkt-Gerade (LF)
Beispiel:
Bestimme den Abstand des Punktes
P
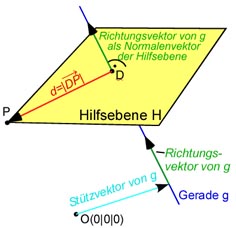 Um den Abstand zwischen Punkt und Gerade zu bestimmen, müssen wir eine Hilfsebene bilden.
Um den Abstand zwischen Punkt und Gerade zu bestimmen, müssen wir eine Hilfsebene bilden.
Diese Hilfsebene ist orthogonal zu unserer Geraden
Der Normalenvektor der Hilfsebene ist also der Richtungsvektor der
Geraden,
Nun berechnen wir den Durchstoßpunkt der Geraden mit der Hilfsebene.
Gesucht ist der Durchstoßpunkt zwischen der Geraden g:
Wir setzen einen allgemeinen Geradenpunkt der Geraden
|
|
= |
|
|
|
|
= |
|
|
|
|
= |
|
|
|
|
|
= | |: |
|
|
|
= |
Den Durchstoßpunkt erhalten wir, indem wir dieses t in die Geradengleichung bzw. in den allg. Geradenpunkt
=> D
Der gesuchte Abstand zwischen dem Punkt P
d=|
Abstand zweier windschiefer Geraden (LF)
Beispiel:
Bestimme den Abstand der beiden windschiefen Geraden
g:
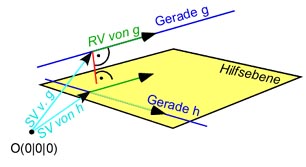 Zuerst bilden wir eine Ebene, welche die Gerade h:
Zuerst bilden wir eine Ebene, welche die Gerade h:
Der Normalenvektor dieser Ebene ist der Normalenvektor auf die beiden Richtungsvektoren der Geraden.
Wenn wir den Aufpunkt von h Ah
Nun können wir den Abstand zwischen der Geraden g:
Wir berechnen den Abstand zwischen Punkt und Ebene mittels der Hesse'schen Normalenform.
Abstand windschiefer Geraden mit Lotfußpunkte (LF)
Beispiel:
Bestimme den Abstand der beiden windschiefen Geraden
g:
Bestimme zusätzlich die Koordinaten der beiden Lotfußpunkte, also jener Punkte, auf den beiden Geraden, die den kleinsten Abstand zueinander haben;
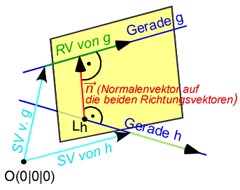 Wir bilden zunächst den Normalenvektor auf die Richtungsvektoren der beiden Geraden.
Wir bilden zunächst den Normalenvektor auf die Richtungsvektoren der beiden Geraden.
Nun stellen wir eine Hilfsebene auf, welche die Gerade g:
Diese Ebene formen wir nun in die Koordinatenform um. (Detail-Rechnung einblenden)
Nun bestimmen wir den Durchstoßpunkt der Gerade h:
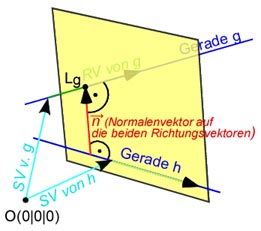 Das ganze Spiel führen wir für den zweiten Punkt erneut durch. Wir stellen eine Hilfsebene auf,
welche diesmal die andere Gerade h:
Das ganze Spiel führen wir für den zweiten Punkt erneut durch. Wir stellen eine Hilfsebene auf,
welche diesmal die andere Gerade h:
Auch diese Ebene formen wir nun in die Koordinatenform um. (Detail-Rechnung einblenden)
Jetzt bestimmen wir den Durchstoßpunkt der Geraden g:
Schlussendlich bestimmen wir den Abstand zwischen diesen beiden Lotfußpunkten Lh
d=|
Ebene mit best. Abstand zu paral. E
Beispiel:
Gegeben ist die Ebene E:
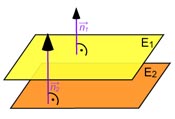
An der Abbildung rechts erkennt man, dass eine zu E parallele Ebene den gleichen Normalenvektor
Um das d noch zu bestimmen, brauchen wir einen Punkt auf der Ebene F. Diesen können wir bestimmen, wenn wir auf den Ortsvektor eines beliebigen Punkt PE einen Normalenvektor der Länge d=24 draufaddieren (weil der Normalenvektor ja orthoginal zu E und F ist.)
Dazu suchen wir zuerst mal einen beliebigen Punkt der Ebene E, z.B. einen Spurpunkt PE
Die Länge des Normalenvektors berechnen wir mit |
Wenn wir also von PE
Jetzt können wir diesen PF in die die Koordinatengleichung
Die gesuchte Ebene ist also F:
Flächeninhalt Trapez
Beispiel:
Gegeben ist das Viereck ABCD mit A
Zeige, dass ABCD ein Trapez ist.
Berechne den Flächeninhalt des Trapezes ABCD.

Wegen
Um den Flächeninhalt dieses Trapezes zu berechnen, müssen wir den Mittelwert der beiden parallelen Seiten mit der Höhe h, also dem Abstand
der beiden parallellen Strecken multiplizieren:
A =
Mit
Die Höhe des Trapez h berechnen wir durch den Abstand der beiden parallelen Seiten, also durch den Abstand des Punkts C von der Geraden durch A und B:
Somit ist der Höhe im Trapez h = 3 und damit
A =
Lotfußpunkt einer Gerade zu P
Beispiel:
Bestimme den Punkt auf der Geraden g :
 Der Punkt auf g mit dem kleinsten Abstand zu einem Punkt P
Der Punkt auf g mit dem kleinsten Abstand zu einem Punkt P
Da diese Hilfsebene H orthogonal zu unserer Geraden
d =
Somit gilt: H:
Da ja der gesuchte Lotfußpunkt sowohl auf der Gerade g als auch auf der Hilfsebene H liegt, können wir diesen als Durchstoßpunkt der Geraden g mit H berechnen:
Wir setzen einen allgemeinen Geradenpunkt der Geraden
|
|
= |
|
|
|
|
= |
|
|
|
|
= |
|
|
|
|
|
= |
|
|: |
|
|
= |
|
Den Durchstoßpunkt erhalten wir, indem wir dieses t in die Geradengleichung bzw. in den allg. Geradenpunkt
=> L
Abst. windschiefer Geraden (rückwärts)
Beispiel:
Gegeben ist eine Geradenschar ga durch
Für welche Werte von a, hat die Gerade ga den Abstand
Die x3-Achse hat die Geradengleichung
Wie immer beim Abstand zwischen zwei windschiefen Geraden benötigen wir jetzt einen Normalenvektor zu den beiden Richtungsvektoren, also einen Vektor, der orthogonal zu beiden
Richtungsvektoren liegt. Weil ja der Richtungsvektor von ga eine 0 in der x3-Koordinate hat, ist der Vektor
Man sieht schnell, dass t = 0 sein muss,
damit auch
(Natürlich hätte man den Normalenvektor auch mit dem Vektorprodukt (Kreuzprodukt) berechnen können)
Jetzt kann man den Abstand zwischen den beiden windschiefen Geraden (ga und die x3-Achse) mit der Formel berechnen:
Im Zähler steht das Skalarprodukt vom Verbindungsvektor der Aufpunkte der Geraden mit dem Normalenvektor, im Nenner der Betrag des Normalenvektor
Weil zwei Brüche genau dann gleich sind, wenn ihre Kehrbrüche gleich sind, können wir statt
|
|
= |
|
|
|
|
= |
|
|⋅ 12 |
|
|
= |
|
|(⋅)2 (Vorsicht: evtl. Vergrößerung der Lösungsmenge) |
|
|
= |
|
|
|
= |
|
|
|
|
|
= | |
|
|
| a1 | = |
|
=
|
| a2 | = |
|
=
|

